合同条件と相似条件の似ているところと、違うところを中心に復習していくよ。 三角形の合同条件と相似条件を3つの種類にまとめてみた 三角形の合同条件と相似条件をうまく覚えるために、3つの種類に分類してみたよ。 3つの何かが等しい条件合同, 作図, 相似三角形, 相似変換, 移動・変換 いろいろ動かしてみたら、これと同じものを自分で作成してみましょう。 作図は簡単です。 作図することで身体で理解することができます。 拡大や縮小をして重なる図形は相似であると言います。 拡大相似の表し方を理解する。 (1) ・2つの三角形が相似であるか どうかを判断し,記号∽を用 いて表すことができる。 ワークシート 自己評価表 三 ・相似の位置や相似の中心を理 解し,相似な図形の性
相似の問題です 画像の図形を 点oを相似の中心として 1 5倍に拡大した図形 Yahoo 知恵袋
相似の中心とは
相似の中心とは-相似の位置、相似の中心とはなんですか? 2つ 簡単作図相似の中心を使って拡大図をかく5 相似とは コトバンク;円の中心の作図方法 まとめ お疲れ様でした! 円の中心の作図は全然難しいものではありませんでしたね。 中心は、円周上のどの点からも等しい距離にある。 垂直二等分線を利用すると、2点から等しい距離にある点が作図できる。




中3数学 拡大図 縮図の作図 練習編 映像授業のtry It トライイット
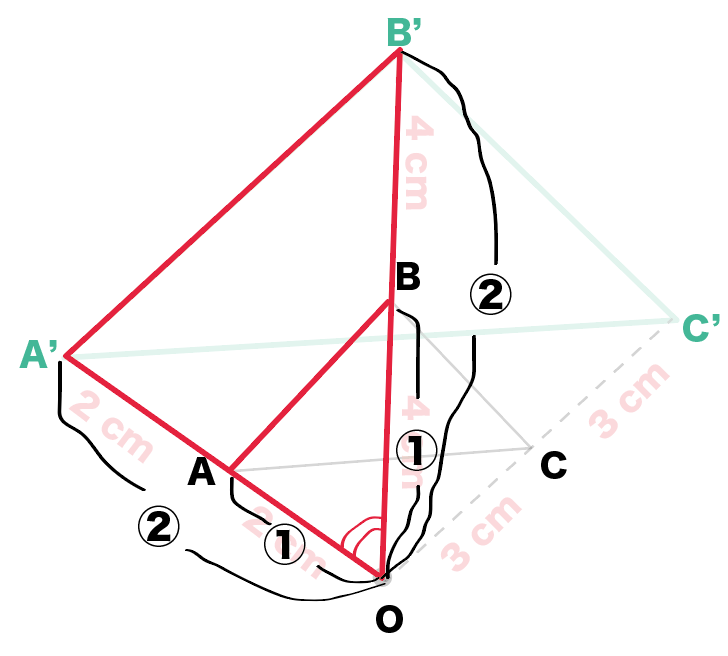
中学3年生では初めての図形の単元です。 相似な図形のかき方、三角形の相似条件や、相似を利用した距離や高さの求め方を練習していきます。 2年生の「 合同と証明 」などを軽くおさらいしてから取り組むと良いでしょう。 相似な図形(1) ⇒ 答えPとaとa'の3点を通る円、pとbとb'の3点を通る円を描く。この2つの円の交点oが不動点になる。図2が作図の例であるが、 oabと oa'b'が相似の関係になっていてoを中心に縮小させながら回転すると辺abが辺a'b'に移動することが理解できるであろう 。 その2相似 math005netcom 中3相似の中心を利用した作図
N は相似の中心となる。 n を通る直線 g と円 o の交点を a,b,対応する円 o' 上の点を a',b' とする。4 点 t,t',a,b' および t,t',a',b はそれぞれ同一円周上にある。えて,「相似の位置」や「相似の中心」などを,用語として定義する必要はないと考えました。なお,これらの用語 を取り上げたい場合は,「1つの点を中心として拡大図をかく」ことのなかで,簡単にふれておくのもよいでしょう。 相似の中心 相似の位置アポロニウスの問題(英 Problem of Apollonius)とは、平面において与えられた3つの円に接する円を描く問題である。とても面白い問題で、普通は8本あるが、いくつあるのかをフリーハンドで作図す
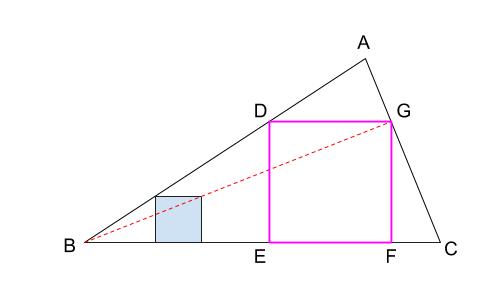
2 学校数学における相似 Research Institute for 相似の中心と作図 ;相似の位置・相似の中心とは イ 三角形の相似条件を用いた図形の性質の論証 ・ 対応する辺の混乱防止方法 ウ 平行線と線分の比 ・ 平行線と線分の比 (仮定理) ・ 平行線で区切られた線分の比の定理 ① 線分の比と平行線 (平行線と線分の比の逆) ・作図の方針は、相似の中心の利用です。 下図が作図の全容です。 水色の小さい正方形と、赤い正方形 \(defg\) が相似です。 点 \(b\) が相似の中心となっています。 つまり、 水色の正方形を作図すれば、 点 \(g\) の位置が確定できるのです。



Http Www Kumamoto Kmm Ed Jp Sugakubraindumps Pdf 3 5 Answer Pdf



中学3年 数学 相似の中心と作図 Cmovie 教育に特化した無料動画サイト シームービー オンライン学習サイト
Centre of similarity 相似中心 centre of similitude 相似中心 centre 中心;心 基于42个网页相关网页A 、所有的矩形都是相似形 b 、 有一个角等于1000 的两个等腰三角形相似 c 、对应角相等的两个多边形相似 d 、对应边成比例的两个多边形相似 ⒊在直角三角形abc 中,∠acb=90°,cd ⊥ab 于d ,若ad=1,bd=4,则 cd=( )a 、2 b 、4 c 、2 d 、3 ⒋Translations in context of "homotheticcenter" in EnglishJapanese from Reverso Context However, if a line Lk does not intersect its circle Ck for some k, there is no pair of solutions for that homotheticcenter line




初等数学模索生活 相似な図形 1



第5章16 相似の応用 三角形の重心 プログラミングの雫
3 相似の位置にある図形を考え、いろ ・北海道の作図がどうしてかけたのかを考察するこ 1点を中心として相似な表現・処理 いろな方法でかく。 相似な図形を作図する とにより相似の位置にある図形のかき方を考え 図形をかいている。共通接線にまつわる発展的な話題 2つの円の共通内接線の交点,共通外接線の交点は相似の中心になっています(相似の中心に関しては 接する2つの円の相似の中心 参照)。相似の位置 ここから,数回相似変換を中心に扱います.相似は平面図形の中で, 豊富な内容を含む分野の一つです.しかし,案外扱いづらく, 中学生,高校生に相似に関する出題をすると,合同の問題に比べて 極端にできなくなります.また,相似は図形に対する洞察力を調べるのに
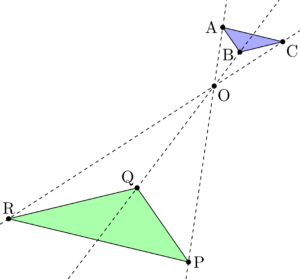



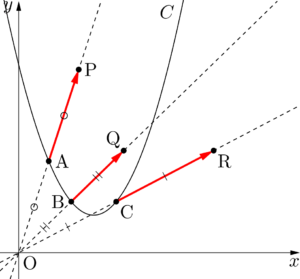
すべての放物線が相似であることの証明 大学入試数学の考え方と解法



2
相似な図形とは?中学3年数学 相似比と辺の比中学3年数学 相似の位置と中心中3数学 相似な図形や中心の作図中3数学 三角形の相似条件中3数学 相似な三角形の辺の比中3数学 21相似の証明 相似の証明の基本その1中3数学放物線が相似であることの証明 y=ax^2bxc y = ax2 bx c のグラフとして表される放物線たちは,強い意味で,すなわち回転を許容しない相似です。 任意の2つの放物線に対して相似の中心が存在して,一方は他方の拡大(縮小)になっています。 ただし,相似の中心を求めるのは計算がめんどうなので,ここでは2つの放物線が定義2Aを満たしていることを証明します。1. 1次変換(線形変換)とは (1) 写像のうちで同一集合から同一集合への対応となっているものを 変換 といいます. (2) 平面上の点 (x, y) を点 (x', y' ) に移す変換 f が次の式で表されるとき,この変換 f を 1次変換(線形変換) という. f x'=axby ・・・①



平面の変換
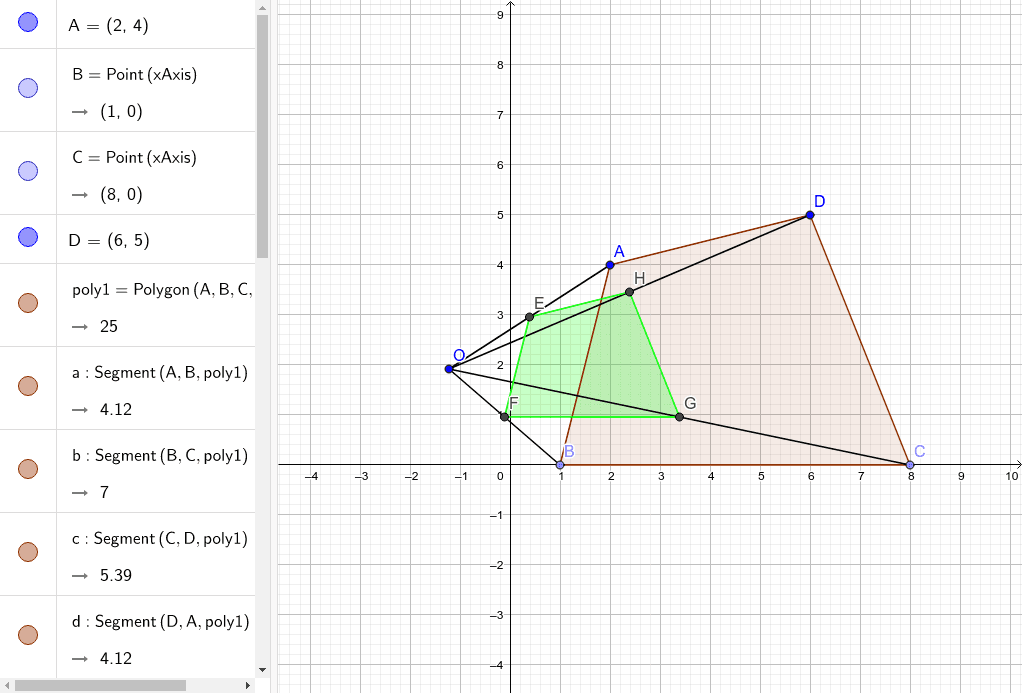



相似の中心の移動 Geogebra
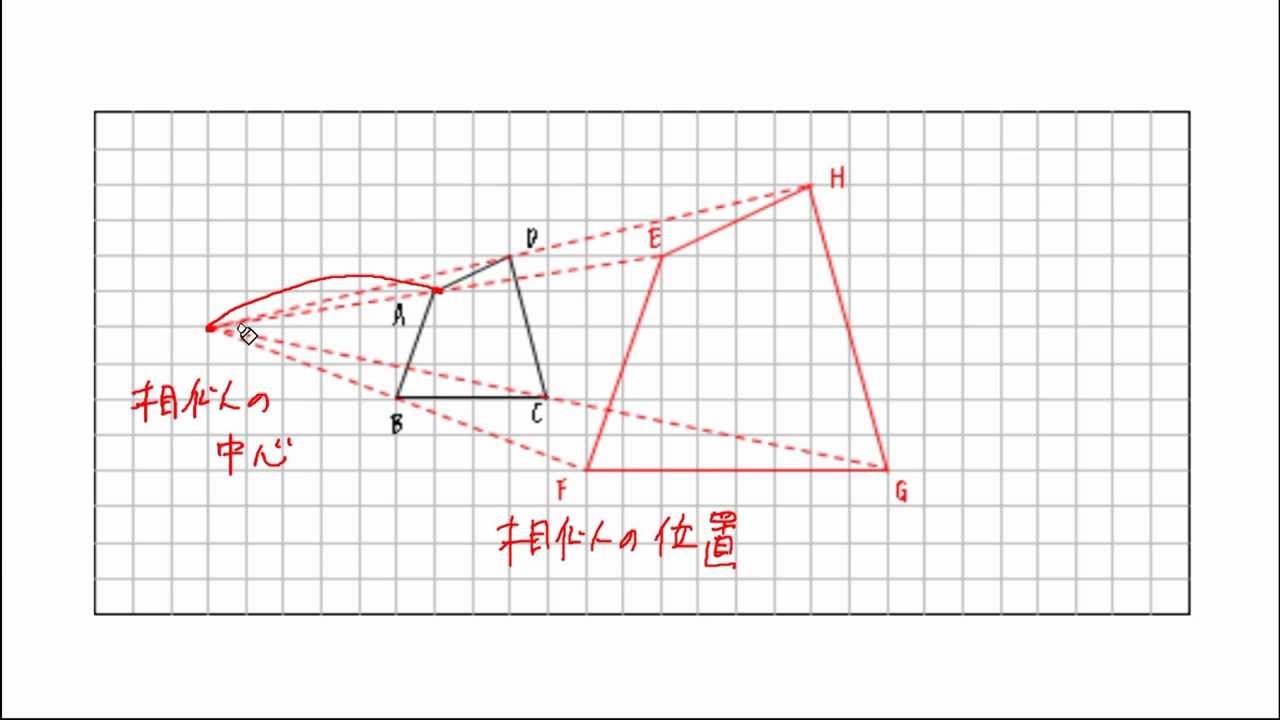
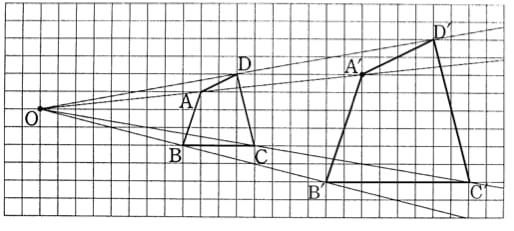
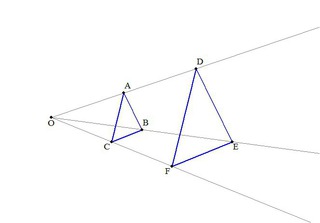
相似の中心o が三角形の内部にあるときも同様である。 下の図は,点o を中心として,4abc を3 倍に拡大した 4def をかいたもので,どちらの場合でも4abc と4def は相似の位置にある。 a d e f b c o a d e f b c o oa od,ob oe,oc of がどれも1 3 になっている ことを確かめよう。A 、所有的矩形都是相似形 b 、 有一个角等于1000 的两个等腰三角形相似 c 、对应角相等的两个多边形相似 d 、对应边成比例的两个多边形相似 ⒊在直角三角形abc 中,∠acb=90°,cd ⊥ab 于d ,若ad=1,bd=4,则 cd=( )a 、2 b 、4 c 、2 d 、3 ⒋相似変換そうじへんかんsimilar transformation 平面上の点 ( x , y) をほかの点 ( x ′, y ′) へ移す変換 は,点 ( x , y) を,原点のまわりに角 θ だけ時計の針の進む方向に回転させ,平面を原点から一様に引延ばして,各点 ( x , y) を原点からもとの距離の k 倍



相似の位置 相似の中心とはなんですか 2つの図形の対応す Yahoo 知恵袋



2
したがって、相似の中心は、S(-2,-2) で、相似比は、2 : 1 であることが分か る。(終) 上記の2つの放物線と相似の中心を図示すれば、下図のようになる。30 例題一:下列各題中,請以o 為縮放中心,畫出四邊形abcd 縮放3 倍的 圖,並比較兩小題所畫出來的縮放圖,它們對應角的角度是否相同? (1) (2) 比較後會發現第(1)小題的縮放圖會與第(2)小題的縮放圖一2つの図形は相似になっており ab:cd=6:9=2:3より 相似比は2:3だと分かります。 つまり、他の辺の比も2:3になるので ae:de=be:ce=2:3 とわかります。 このae:de=2:3ということを利用して 次は、 adbと edfに注目すると



3
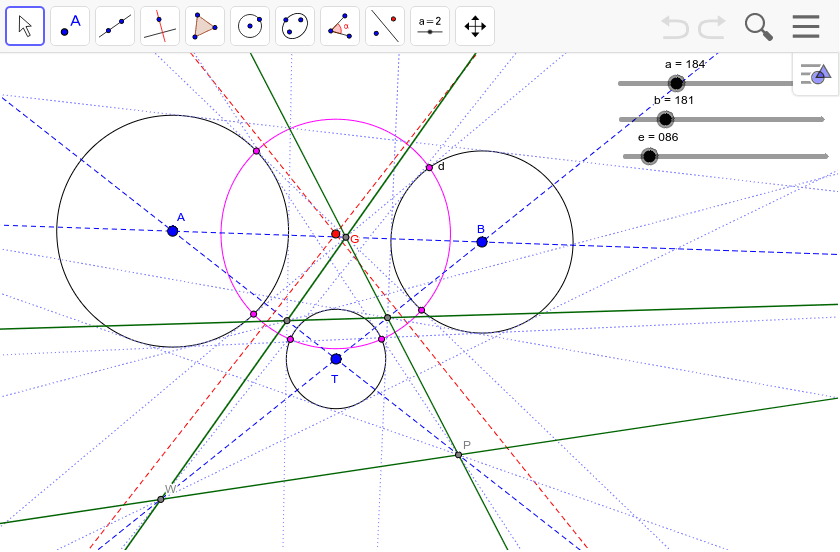



2つの円の相似の中心 Geogebra
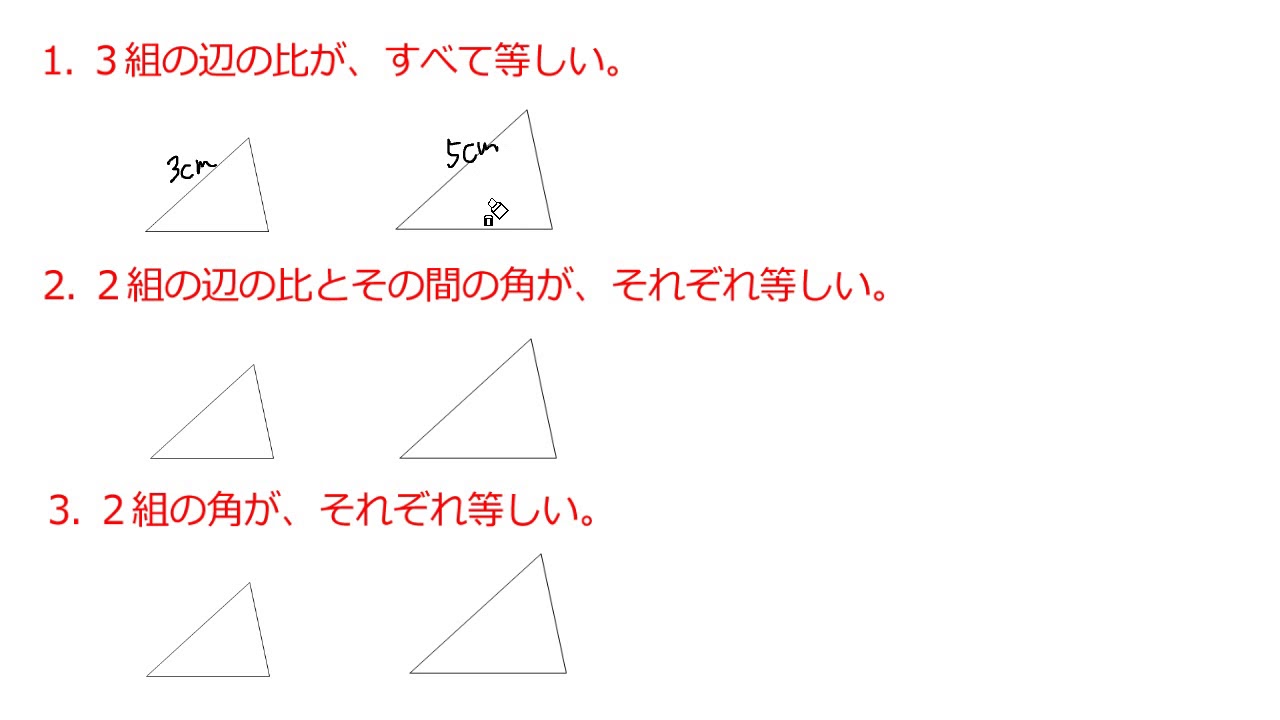
三角形の相似条件 相似の問題の中でも、三角形の相似を証明する問題が多く出題されます。 ここでは、三角形の相似を証明するために必要な3つの条件を説明します。 私が実際に問題を解いた時に使う回数が多いと感じた順に書いてみました。 1つめは




相似 作図 この問題の解説の 赤丸ぶぶんがよく分からないです Clear



平面の変換




F3 相似の中心 相似の位置 定義 Geogebra




Kelas 9 Catatan Tentang 中学3年 Clear



九点円



2




相似な図形 Ict教材eboard イーボード



相似の中心 相似の位置 とはいったいなんですか 2つの相 Yahoo 知恵袋



相似な図形 確認問題 苦手な数学を簡単に



平面の変換



放物線の相似性




中学数学 理科 寺子屋塾の復習サイト 相似な図形
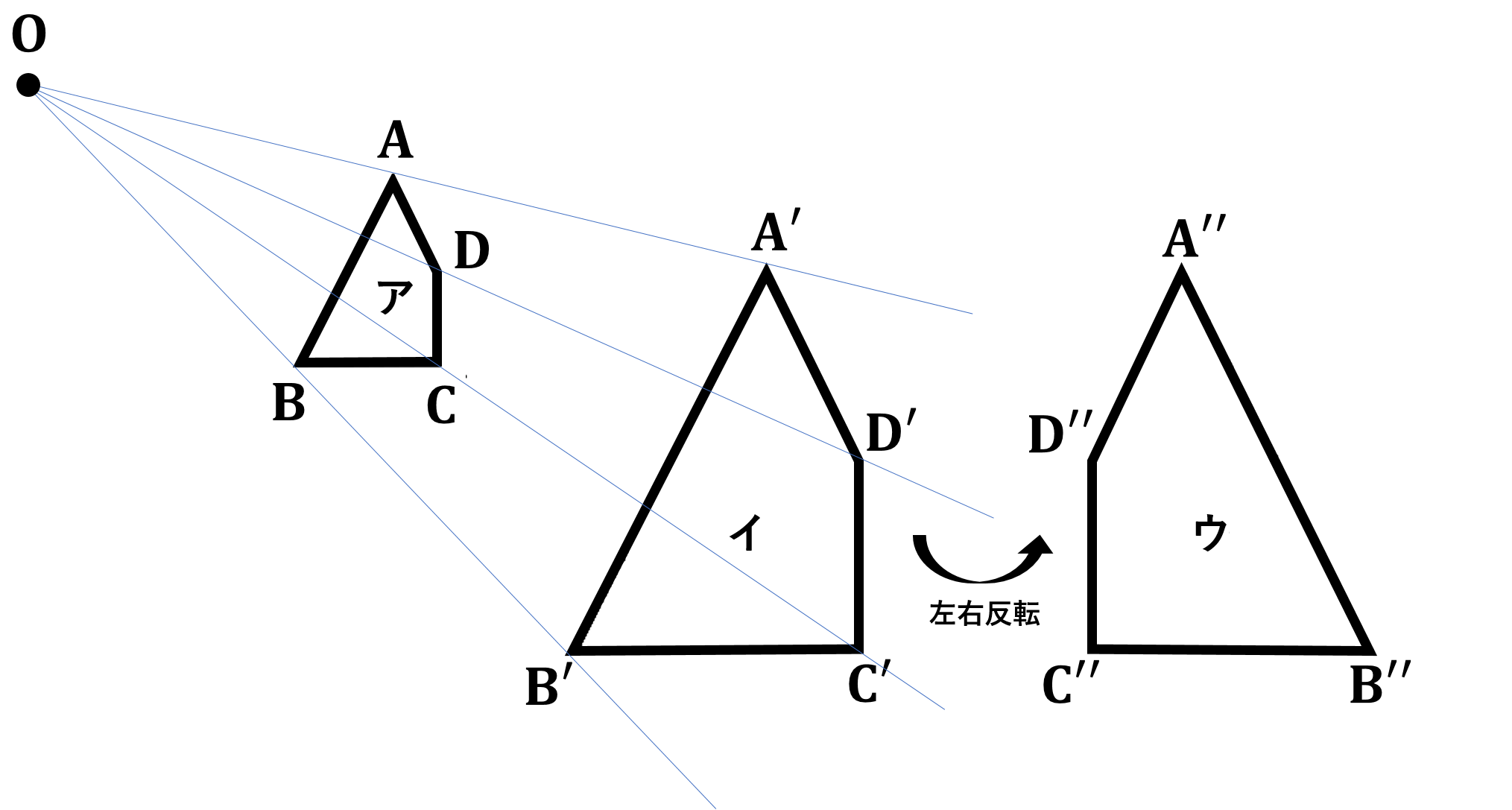



5章 相似 タカラゼミ



Top
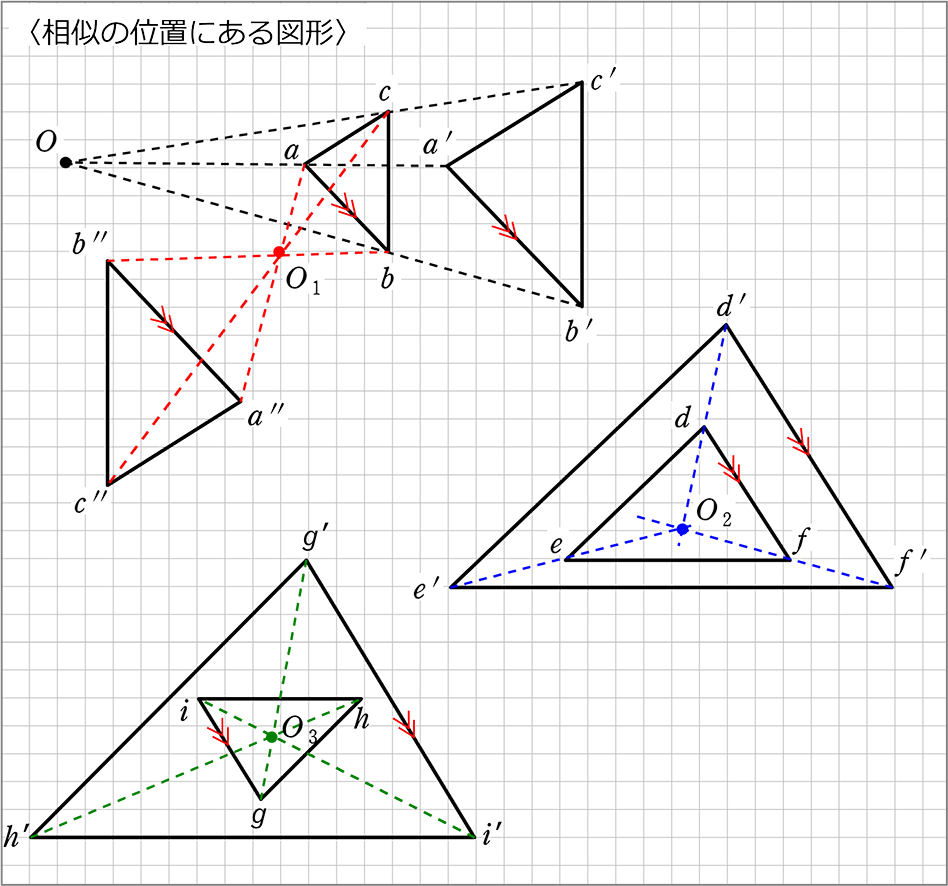



中学数学 図形の相似




円の相似拡大 縮小 Etc Den Of Hardworking



Http Www Criced Tsukuba Ac Jp Renkei Msa Lessonplan Ooneda 2nd Medio Ooneda07 Jap Pdf




相似の中心と作図 Youtube




中3数学 拡大図 縮図の作図 練習編 映像授業のtry It トライイット




図形と相似 1 きっずゼミ子育て応援ブログ



Studydoctor相似な図形や中心の作図 中3数学 Studydoctor




三角形の相似条件が見やすい図で一発理解できる 練習問題付き 高校生向け受験応援メディア 受験のミカタ



1



相似の応用 規則集3 中学から数学だいすき



高校入試 英語 数学 図形と相似 相似の基礎




スプリックス 相似の位置と相似の中心 6 Youtube



簡単作図 相似の中心を使って拡大図をかく5つのステップ Qikeru 学びを楽しくわかりやすく




赤い三角のところがなぜそうなるのかが理解できません Clear




中3数学 拡大図 縮図の作図 映像授業のtry It トライイット



相似な図形 Ict教材eboard イーボード



相似の中心と作図 Youtube



16年前期 千葉県公立高校入試 数学 第2問 5 作図 解答 解説 船橋市議会議員 朝倉幹晴公式サイト



Http Www Pref Chiba Lg Jp Kyouiku Shidou Gakuryoku Yaruki Suugaku Documents M3012 Pdf
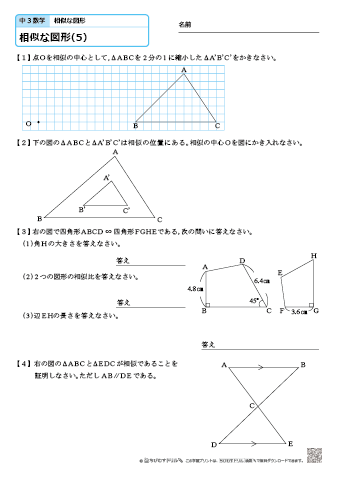



中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




3 解説見ても分からないんですけど もっと分かりやすい解き方ないですか Clear



3



相似の問題です 画像の図形を 点oを相似の中心として 1 5倍に拡大した図形 Yahoo 知恵袋



図形の拡大 縮小2
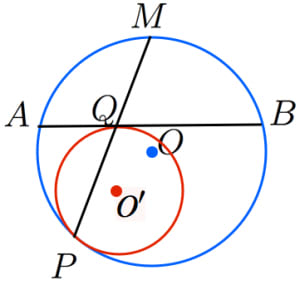



接する2つの円の相似の中心 高校数学の美しい物語



簡単作図 相似の中心を使って拡大図をかく5つのステップ Qikeru 学びを楽しくわかりやすく




相似な図形 相似な図形 1 を教えてください Clear



平面の変換



Studydoctor相似の位置と中心 中3数学 Studydoctor



相似下の方顔用紙に四角形abcdを点oを相似の中心として 2倍に拡大した四 Yahoo 知恵袋




簡単作図 相似の中心を使って拡大図をかく5つのステップ Qikeru 学びを楽しくわかりやすく




相似な図形 Ict教材eboard イーボード



平面の変換
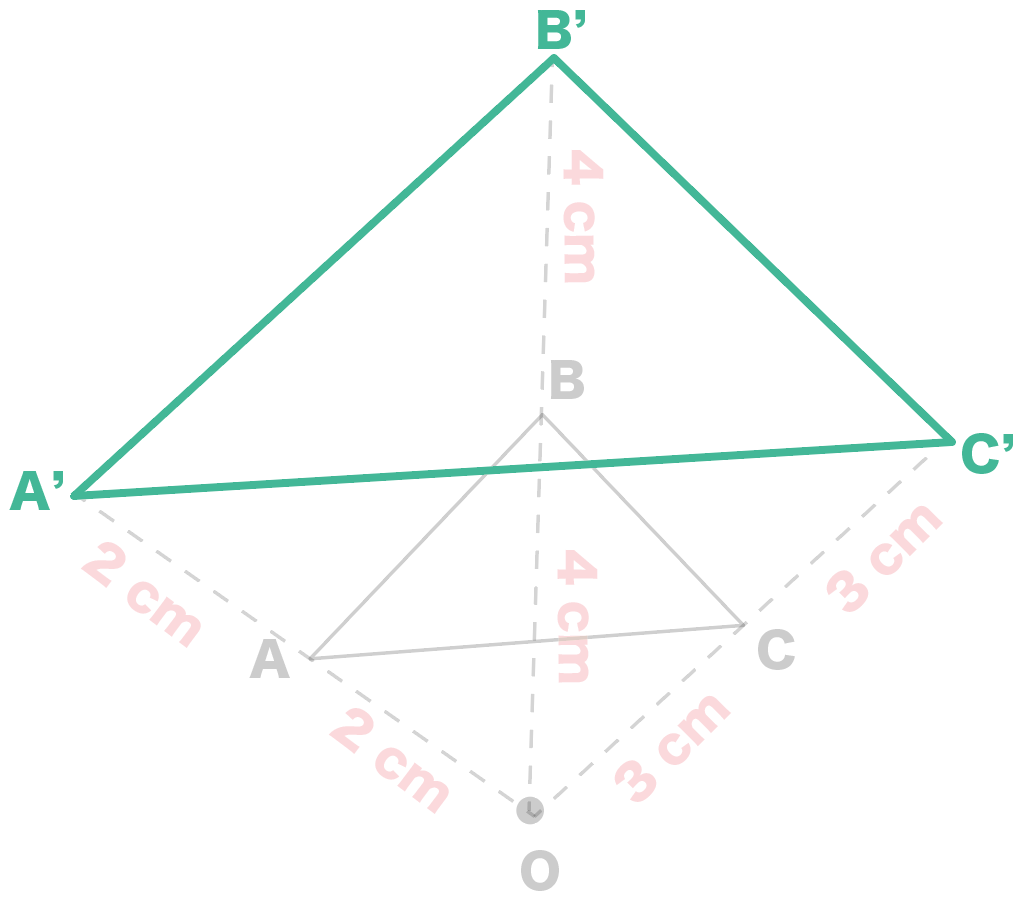



簡単作図 相似の中心を使って拡大図をかく5つのステップ Qikeru 学びを楽しくわかりやすく



平面の変換



相似の例題解説 01 相似な図形 操作 目次の項目 をクリックすると 解答画面に行きます Rei1 Jpg 解答画面 拡大縮小の図形シミュレーター Rei011 Jpg 02 相似な図形のかき方 Rei2 Jpg 03 相似な図形のかき方 Rei3 Jpg 04 相似な図形の



すべての放物線が相似であることの証明 ページ 2 大学入試数学の考え方と解法




中3数学 拡大図 縮図の作図 練習編 映像授業のtry It トライイット



Http On Study Jp Math 3 23 Pdf



Happylilac Net Pdf Jhs Math3 05 01ans Pdf



Http Www Rs Tottori U Ac Jp Mathedu Mt Xue Sheng Zuo Pin Files 11 Shukuzu 26kakudaizu Pdf




中3数学 拡大図 縮図の作図 練習編 映像授業のtry It トライイット



Www Kyoiku Shuppan Co Jp Textbook Shou Sansu Files 2540 27 H27 Renkei 3 Pdf



作図 相似の中心の利用 中学数学の無料オンライン学習サイトchu Su
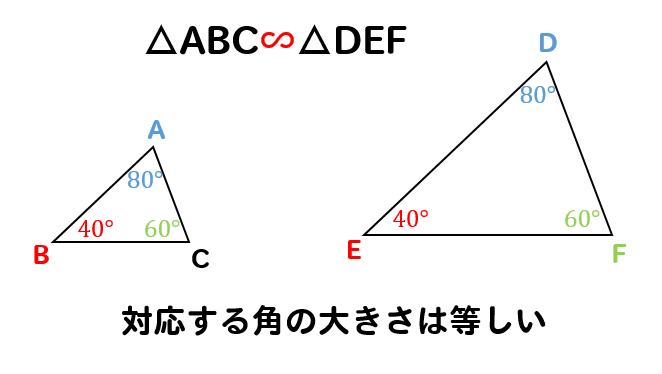



中3数学 相似の基本性質をわかりやすく問題解説 数スタ



放物線の相似性




相似 作図 この問題の解説の 赤丸ぶぶんがよく分からないです Clear




根軸 Wikipedia



Www Shinko Keirin Co Jp Keirinkan Chu Math Support Keyseat Data Sugaku 3nen2 02 Pdf



Http Www2 Gsn Ed Jp Houkoku 03c 03c07 03c08s Pdf
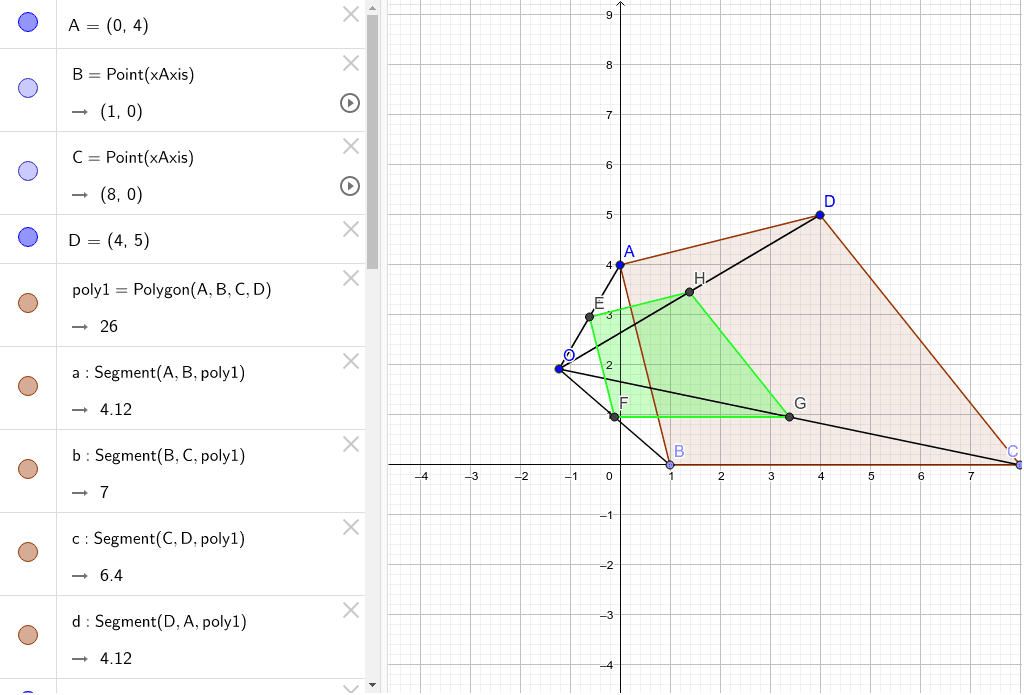



相似の中心の移動 Geogebra



数学の相似の図形の問題です分かる方 この問題の答えを教えてくださいこの Yahoo 知恵袋



相似1 Takapの数学日記



中学校数学 3年生 図形 相似な図形 Wikibooks



簡単作図 相似の中心を使って拡大図をかく5つのステップ Qikeru 学びを楽しくわかりやすく



簡単作図 相似の中心を使って拡大図をかく5つのステップ Qikeru 学びを楽しくわかりやすく
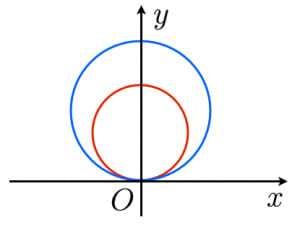



接する2つの円の相似の中心 高校数学の美しい物語
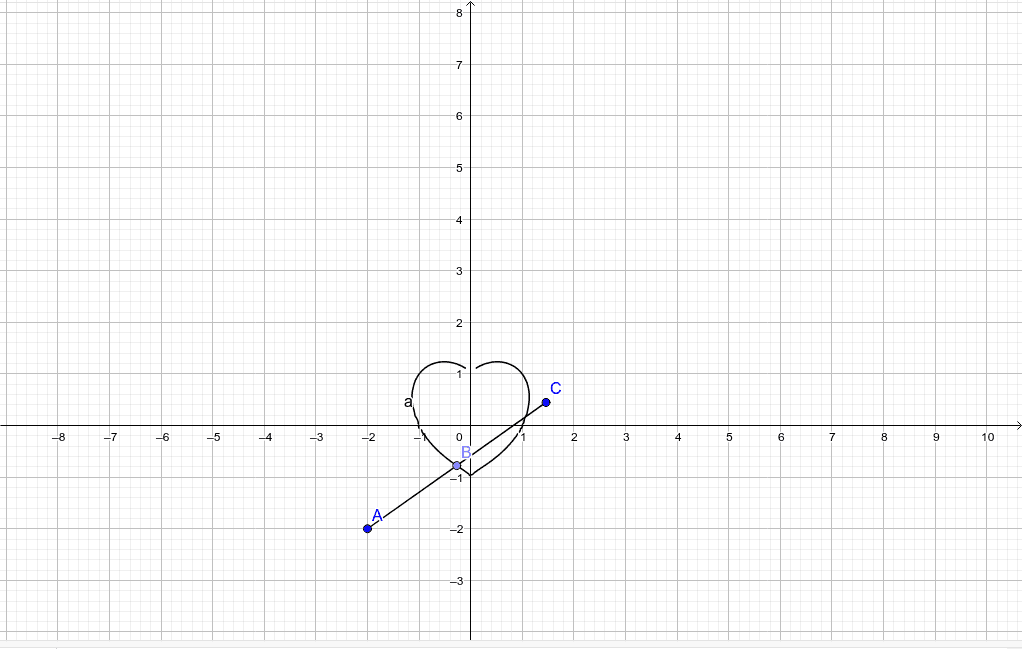



F3 相似の中心 ハート Geogebra
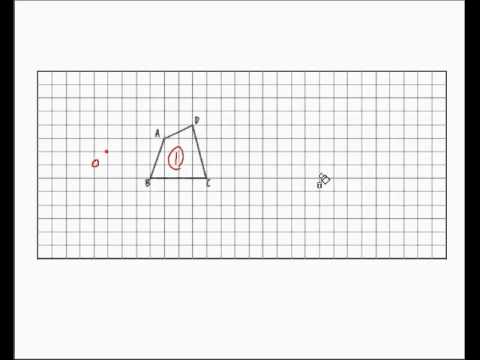



相似の中心と作図 Youtube
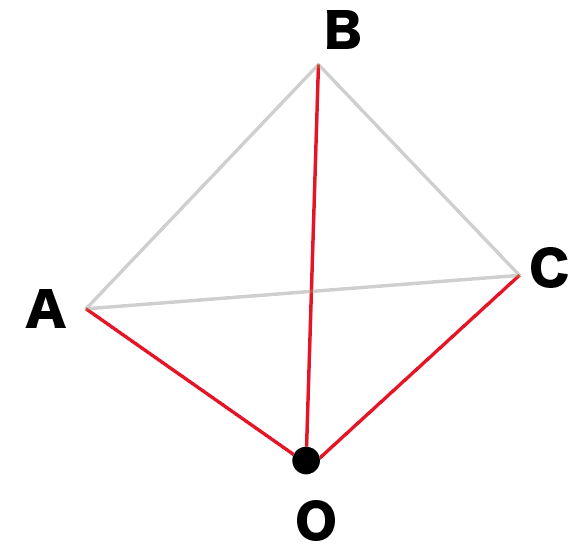



簡単作図 相似の中心を使って拡大図をかく5つのステップ Qikeru 学びを楽しくわかりやすく



Http Www Rs Tottori U Ac Jp Mathedu Mt Xue Sheng Zuo Pin Files 11 Shukuzu 26kakudaizu Pdf



中学校3年 数学 アーカイブ Cmovie 教育に特化した無料動画サイト シームービー オンライン学習サイト



四角形a B C E は点oを相似の中心として四角形abcdを2分の Yahoo 知恵袋



図形の相似 規則集3 中学から数学だいすき



2
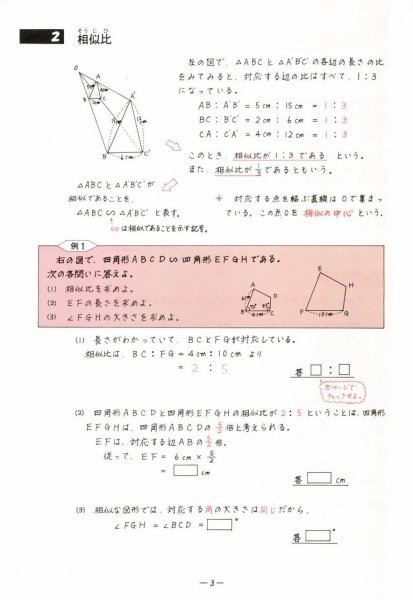



数学単元別シリーズの販売 教材出版 学林舎
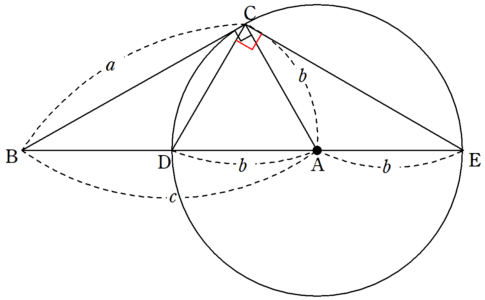



三平方の定理の証明 相似を利用した証明3 Fukusukeの数学めも



Www1 Iwate School Jp Action Common Download Main Upload Id 1428



2




中3 相似の位置と相似の中心 Youtube
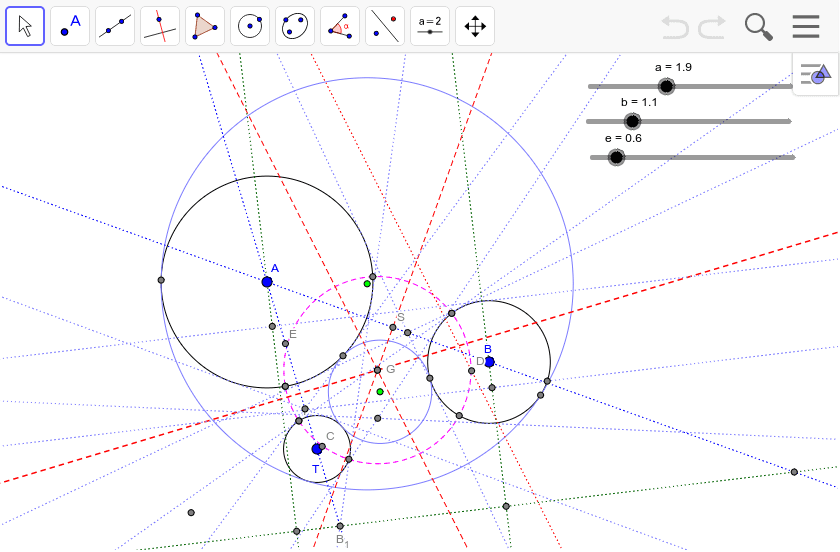



3つの相似の中心を通る線と円との極線 Geogebra




相似な図形 1 例題 きっずゼミ子育て応援ブログ
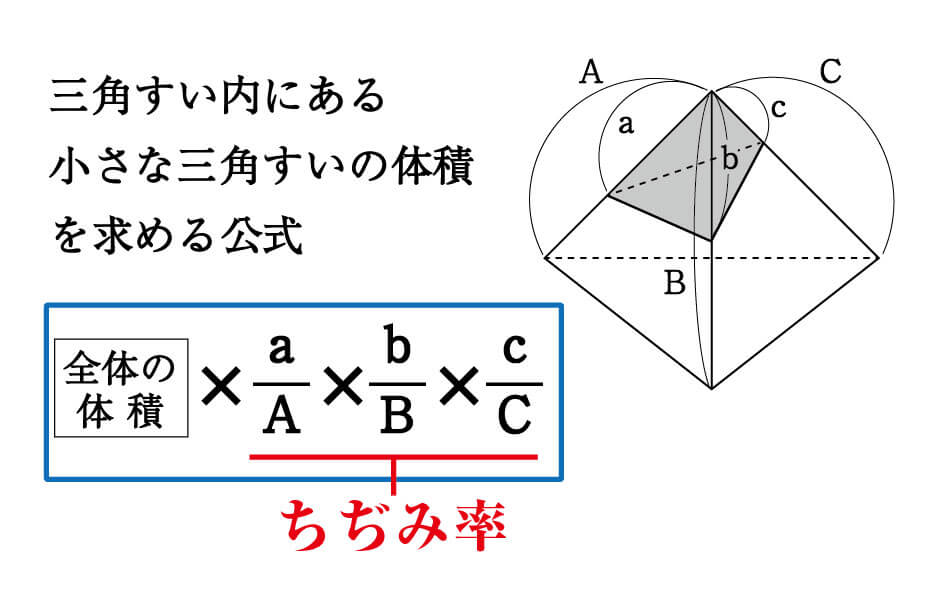



数学 三角錐の体積比を楽に求められる公式 受験の秒殺テク 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



相似の中心 中学から数学だいすき




かみのドリル 相似




相似の中心となる点について 相似の中心となる点についてこんにちは 数学 教えて Goo



相似な図形 Banshot



0 件のコメント:
コメントを投稿