様々な2次方程式の解法(分数、小数、根号、置換、絶対値) 2次方程式では,\ まず {x²の係数を正の整数}にすることが重要である たすき掛けの因数分解は,\ 整数係数でなければ困難だからである 解の公式を使うにしても,\ 分母になるx²の係数が正の整数二項定理 (ab) n の展開式、整式の係数の和 数と式 数と式 連立方程式で3つの式のある3元1次方程式とは? 3元連立方程式の解き方をわかりやすく解説 みなさん、こんにちは。 数学ⅠAのコーナーです。 今回のテーマは3元1次方程式です。 田中くんのように、3元1次方程式と聞くと、すごく

根号
根号を含む式の計算 高校 分数
根号を含む式の計算 高校 分数- 今回は平方根の計算を学ぶ。 定期テストレベルでは、今回までの内容ができれば、 平方根の分野で平均点以上を取れる。 公立高校入試では、大問1の小問集合などでよく出るので、 確実に得点できるようにしておこう。 前回 ←平方根の計算の準備(基) 次回 →平方根の計算(標)高校講座HOME >> 数学Ⅰ >> 第7回 数と式 有理化 数学Ⅰ Eテレ 毎週 月曜日 午後2:10~2:30 ※この番組は、21年度の新作です。 出演者紹介




中3 数学 無料学習プリント教材
根号を含む式の値の求め方とは?←今回の記事 分母の有理化のやり方はこれでバッチリ! ルートの計算方法まとめ!問題を使って徹底解説! ルートの分数計算、問題解説で完全マスターだ! 整数部分、小数部分の求め方!分数の場合には?数と式絶対値記号を含む方程式・不等式の解き方 数と式負の値の絶対値の考え方について 数と式逆・裏・対偶の関係 数と式連立不等式の解の求め方 数と式2重根号の計算;根号を含む式の値の求め方とは? 分母の有理化のやり方はこれでバッチリ! ルートの計算方法まとめ!問題を使って徹底解説!←今回の記事 ルートの分数計算、問題解説で完全マスターだ! 整数部分、小数部分の求め方!分数の場合には?
二項定理 (ab) n の展開式、整式の係数の和いろいろな式 ・整式の乗法,除法 ・分数式の計算 ・二項定理 ・等式と不等式の証明 いろいろな関数 累乗根 平面上の曲線と複素数平面 極限 積分法 <中学校3年> 平方根 平方根 平方根の値 素因数分解 除法 根号を含む式の計算 <中学校1年> 繁分数式 (分数の分数)の計算 分数式の分母または分子がさらに分数式であるもの}}を\textbf {\textcolor {blue} {繁分数式}}という \\ 2zh 本項では,\ 繁分数式の扱いを学習する \\ 1zh 最初に以下の2つの違いを確認してほしい\ \textcolor {red} {横線の長さで区別さ
分数式の加法と減法(基本) 分数式の加法と減法(分子の次数下げ) 分数式の加法と減法(部分分数分解) 繁分数式(分数の分数)の計算;26 二重根号 そこで日本の高校教育では、「項が1つ以上の式」という概念については整式(せいしき)という用語を使っている。 は、分母分子共に整数の分数 根号を含む分数の計算について、 今分母の有理化について勉強しているのですが、 どうしても理解できない問題があります。 √7√3分の√7-√3 上下に同じ数だけかけて分母を有理化することまでは出来るのですが、その後の工程がまったく理解できませ




無料 中3数学 基本解説 解答プリント 314 平方根6 いろいろな計算




平方根 ルート の重要な計算方法まとめ 数学fun
分数式の加法と減法(基本) 分数式の加法と減法(分子の次数下げ) 分数式の加法と減法(部分分数分解) 繁分数式(分数の分数)の計算;(b) 高校で習う分数指数を使って 2^(1/2) と書く方法 があります.(B)の方法を使えば,3乗根,4乗根,・・・なども扱えます.また,結果が分数指数で表される場合もあるので,Maximaで計算するときは,少しは分数指数を理解しておく方がよい.実数と根号(公式と例) 根号計算1 根号計算2 分母の有理化 無理数の独立 式の値 (無理数の対称式) x n 1/x n の値 センター試験問題 平方根の計算 根号計算の入試問題




数 平方根と式の値 高校数学tv Youtube
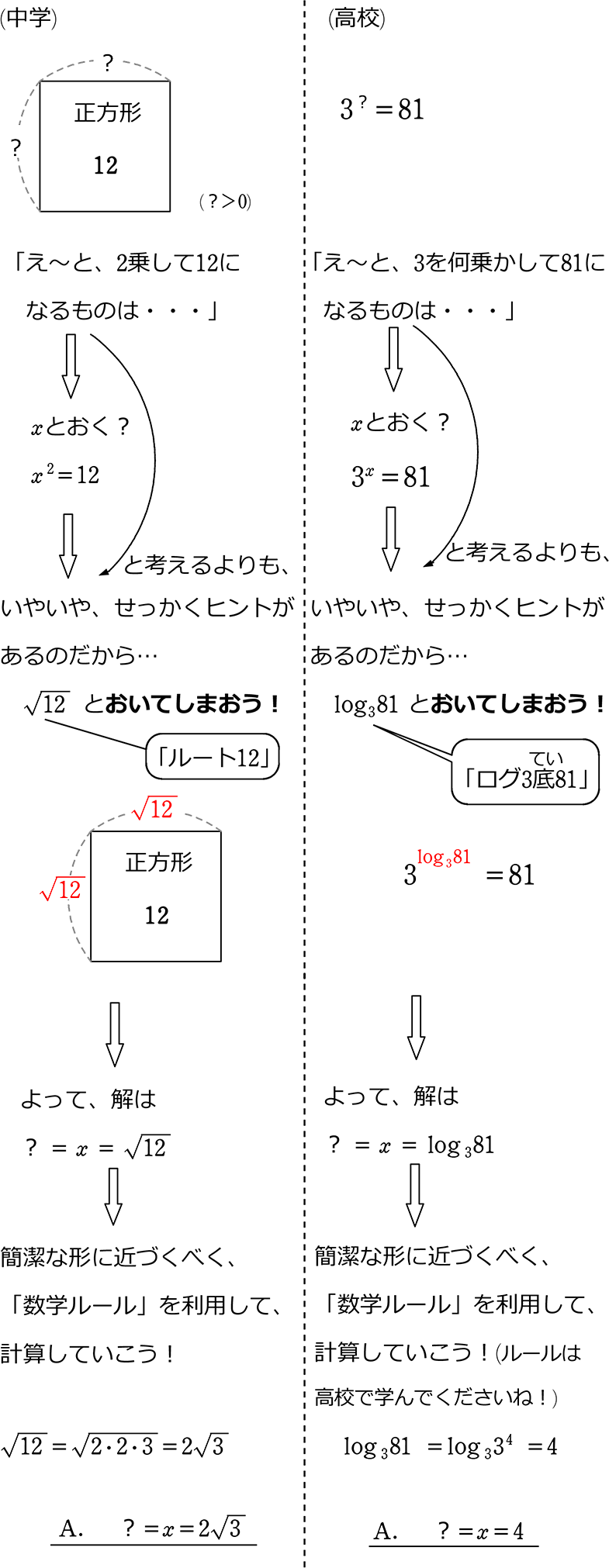



中学数学 平方根
この問題は、根を含む乗法と根を含む除法の2つを組み合わせた式になります。 この計算手順は、 乗法・除法を"根を含まない式と同様に計算する。 素因数分解を実行し、根の外に出せる値があれば出す。 分母に根がある場合は、有理化する。実数と根号(公式と例) 根号計算1 根号計算2 分母の有理化 無理数の独立 式の値 (無理数の対称式) x n 1/x n の値 センター試験問題 平方根の計算 根号計算の入試問題数学i 数と式 実数 根号を含む計算 中学1年 113 高校全般 6 数学i 195 数学a 97 数学ii 260 数学b 100 数学iii 228 高校旧課程 3 大学数学基



最高のコレクション ルート 展開 計算機 ハイキュー ネタバレ




根号
A5判/128頁/定価1650円(本体1500円+税10%)/11年3月発行 ISBN C3041 高校で数学をあまり選択履修してこなかった学生や理解度に自信のない学生向けに,大学で微積などを学ぶ上で欠くことの出来ない基礎知識を,半期の講義用にまとめたリ本時の目標 置換積分により, \(\sqrt{x a}\) を含む無理関数の不定積分を求めることができる。 \(\displaystyle \frac{1}{\sqrt{1 x^2}}\) を含む不定積分を求めることができる。 \(u = x \sqrt{1 x^2}\) の置き換えにより, \(\displaystyle \int \frac{1}{\sqrt{1 x^2}} \,dx\) を求めることができる。根号を含む分数が幾つもある場合,通分よりも分母の有理化の方が有利 類題 を計算せよ. 解説 やり直す (原式) 引用元の問題は記述式の問題ですが,以下の問題ではWeb画面上での操作性をよくするため,選択問題に変えています. まぐれ当たり



1



高校数学 数学 動画で学べるリンク集 家庭学習用プリント学年別リンク集
・根号を含む式の計算 循環小数を表す記号を用いて,分数を循環小数で表 すことができる。 今まで学習してきた数の体系について整理し,考察 しようとする。 絶対値の意味と記号表示を理解している。 根号を含む式の加法,減法,乗法の計算ができる。2節 根号を含む 式の計算 1 根号を含む式の乗法・除法 4時間 (本時3/4時間) 2 根号を含む式の計算 3時間 学習活動 学習内容 数学への関心・ 意欲・態度 数学的な見方や考え 方 数学的な技 能 数量や図形などについての知識・理解 分母に無理 数のある数根号計算(約分) → 携帯版は別頁 2次方程式の解の公式を使うためには,根号計算,特に「根号を含む分数」の約分が正確にできなければなりません.この頁では解の公式を使ったときに登場する「根号を含む分数」の約分を練習します.
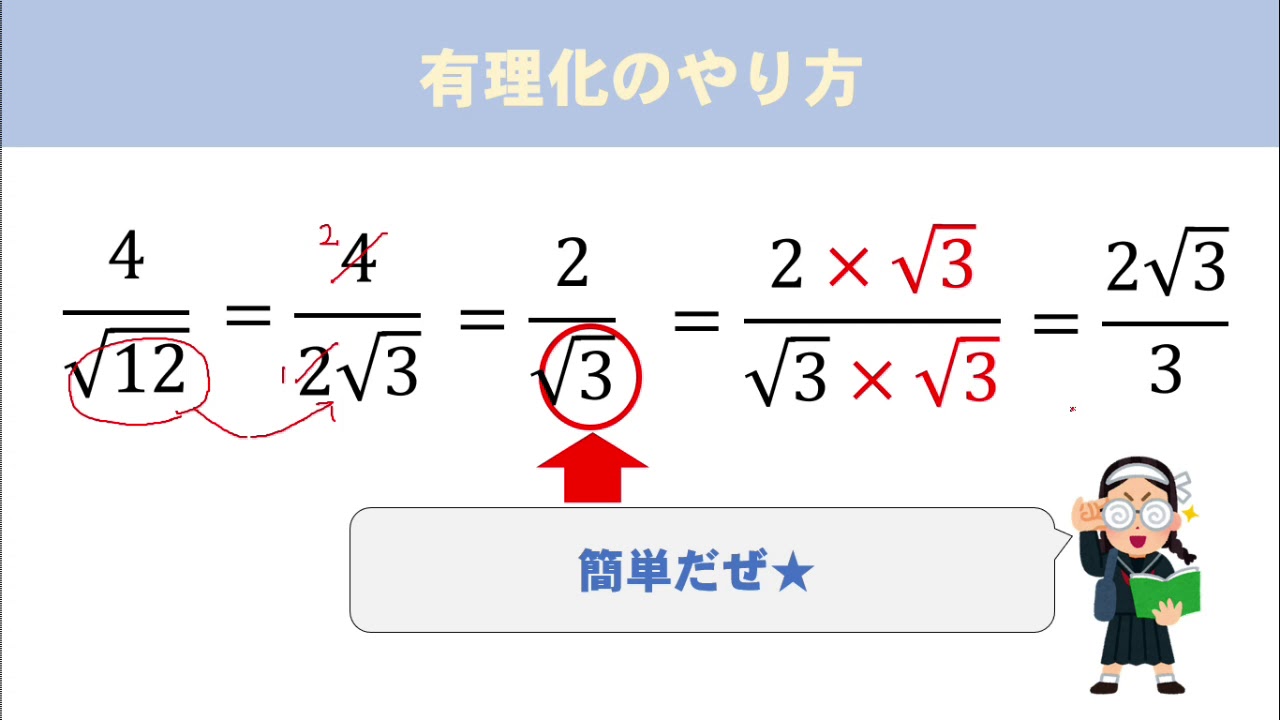



平方根 分母の有理化のやり方はこれでバッチリ 数スタ




数i 3項の有理化 複雑な有理化 Youtube
== 根号計算の入試問題 == ※以下に引用する高校入試問題で,元の問題は記述式の問題ですが,web画面上で入力問題にすると操作性が悪いので,選択問題に書き換えています.根号を含む式の値の求め方とは? 分母の有理化のやり方はこれでバッチリ!←今回の記事 ルートの計算方法まとめ!問題を使って徹底解説! ルートの分数計算、問題解説で完全マスターだ! 整数部分、小数部分の求め方!分数の場合には?小・中学生 高校・専門・大学生・大学院生 主婦 会社員・公務員 自営業 エンジニア 教師・研究員 その他 この計算式は 非常に役に立った 役に立った 少し役に立った 役に立たなかった 使用目的




根号を含む式の計算がわかりません Clear




根号を含む式の計算 しっしーのお計算ん向上委員会
二重根号の外し方のパターンと外せないものの判定 レベル ★ 基礎 式の計算 更新日時 二重根号とは, 5 2 6 \sqrt {52\sqrt {6}} 52 6 のように,ルートの中にルートが含まれているような式



根号 ルートのある式について質問です この問題 答えが分数になら Yahoo 知恵袋




高校数学 根号を含む不等式の証明 受験の月




数学のルートの分数の二乗 この式の計算方法を教えてください 数学 教えて Goo




複雑なルートの分数の有理化のやり方と問題 理系ラボ
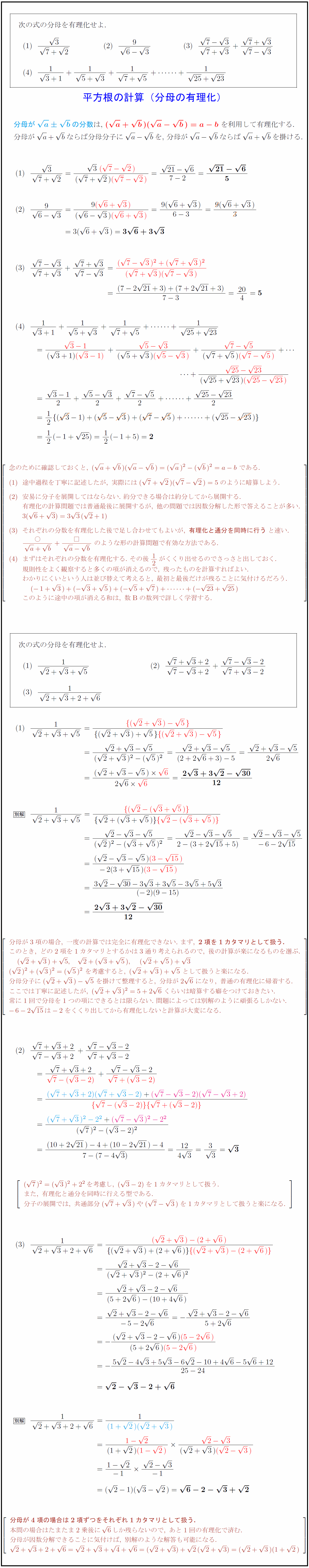



高校数学 平方根の計算 分母の有理化 受験の月




第2講 根号を含む式の計算 1章 2節実数 問題集 高校数学




中学校数学 3年生 数量 平方根 Wikibooks



根号計算 約分




教科書レベルの問題一覧と解答 数学 数と式 教科書より詳しい高校数学




根号を含む式の計算 しっしーのお計算ん向上委員会




7 4 平方根 乗法と除法 勉強できようサイト



根号計算 約分




高校数学 平方根と のおさらい 練習編 映像授業のtry It トライイット



3



1




有理化とは やり方を分かりやすく解説 練習問題つき 高校生向け受験応援メディア 受験のミカタ




数学 定期テストに出題される二重根号を外す問題 大学入試数学の考え方と解法




数と式 平方根について 日々是鍛錬 ひびこれたんれん




数学のルートの分数の二乗 この式の計算方法を教えてください 数学 教えて Goo




有理化とは やり方を分かりやすく解説 練習問題つき 高校生向け受験応援メディア 受験のミカタ
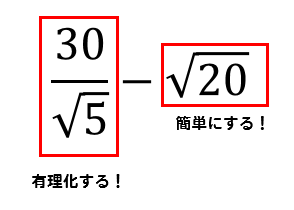



ルートの分数計算 問題解説で完全マスターだ 数スタ




不等号の向きを間違えやすい不等式の計算まとめ わかるようになる高校数学




塾ノート 中3 数学 平方根 中学生 数学のノート Clear




数と式 平方根について 日々是鍛錬 ひびこれたんれん




中3 数学 無料学習プリント教材



1




複雑な二重根号の外し方 タカラゼミ




分数不等式のおすすめの解き方と例題 高校数学の美しい物語




数学 分母にルートの分数がある場合の計算を教えてください 下の計算 数学 教えて Goo




分数計算が得意になる簡単な方法




ルートの分数計算 問題解説で完全マスターだ 数スタ



対称式 平方根通分ルートのある分数の通分の仕方を教えてください Yahoo 知恵袋




根号含む式の計算 高校数学 丸で囲んでるところなのですがなぜ逆にな 高校 教えて Goo



Http Www Fuchu H Metro Tokyo Jp Fuchu Hp Standard H27suugaku 1 Pdf



ルート の分数計算教えてください すみません 急ぎです Yahoo 知恵袋




根号をふくむ足し算と引き算 の分数をふくむ場合 Youtube



平方根 ルート の計算や問題の解き方を完璧に理解しよう Studyplus スタディプラス




第2講 根号を含む式の計算 1章 2節実数 問題集 高校数学




高校数学 繁分数式 分数の分数 の計算 受験の月




ルート 根号 の計算方法をマスターしよう スタディクラブ情報局




平方根の足し算と引き算 ルート計算のやり方や分数の求め方 リョースケ大学



平方根 ルート の計算や問題の解き方を完璧に理解しよう Studyplus スタディプラス




ルートの値を代入する問題 色んな知識を使う良い問題です 中学や高校の数学の計算問題




中3 授業 中3数学 平方根の計算 中学生 数学のノート Clear




中学校数学 3年生 数量 平方根 Wikibooks




ルートに戻す問題 2つの方法を知っていれば 簡単に解くことができる 中学や高校の数学の計算問題




分母に根号を含む分数の計算 まなびの学園




幼児でも分数の加減乗除を習得
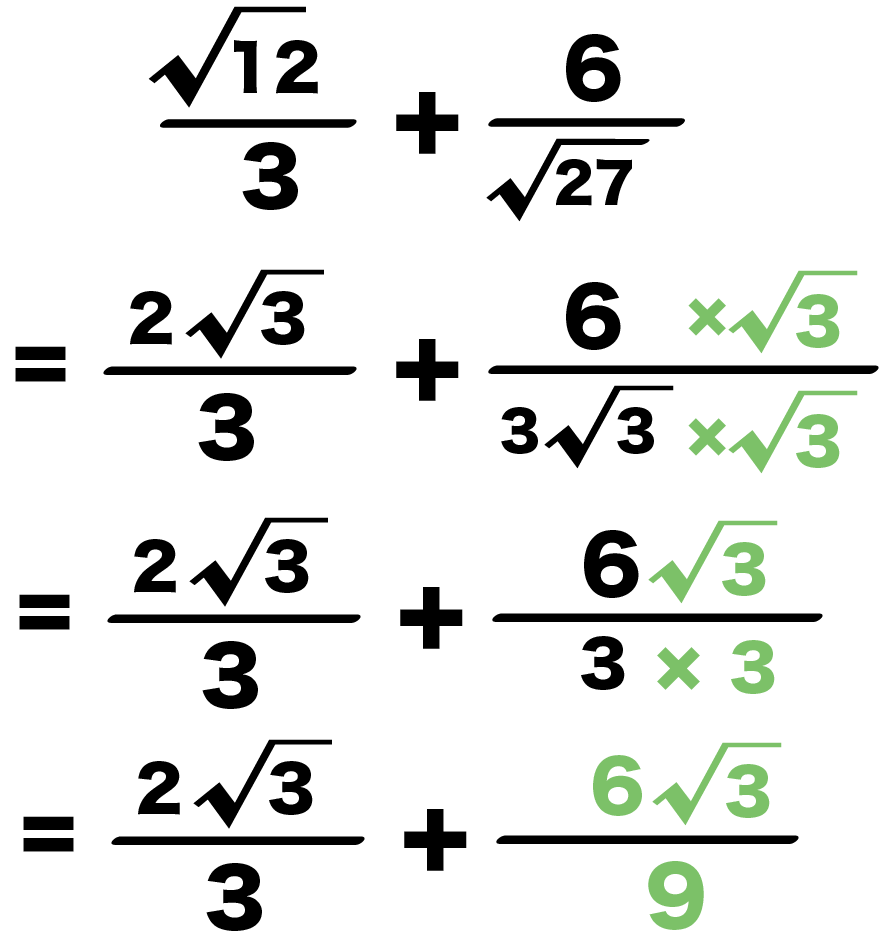



平方根の計算 ルートの分数の足し算 引き算の仕方がわかる5ステップ Qikeru 学びを楽しくわかりやすく




高校数学 数 14 ルート シリーズ 因数分解とのコラボ編 Youtube




7 4 平方根 乗法と除法 勉強できようサイト




第2講 根号を含む式の計算 1章 2節実数 問題集 高校数学




根号を含む式の計算 乗法 除法をくふうして計算する 教遊者




複雑なルートの分数の有理化のやり方と問題 理系ラボ
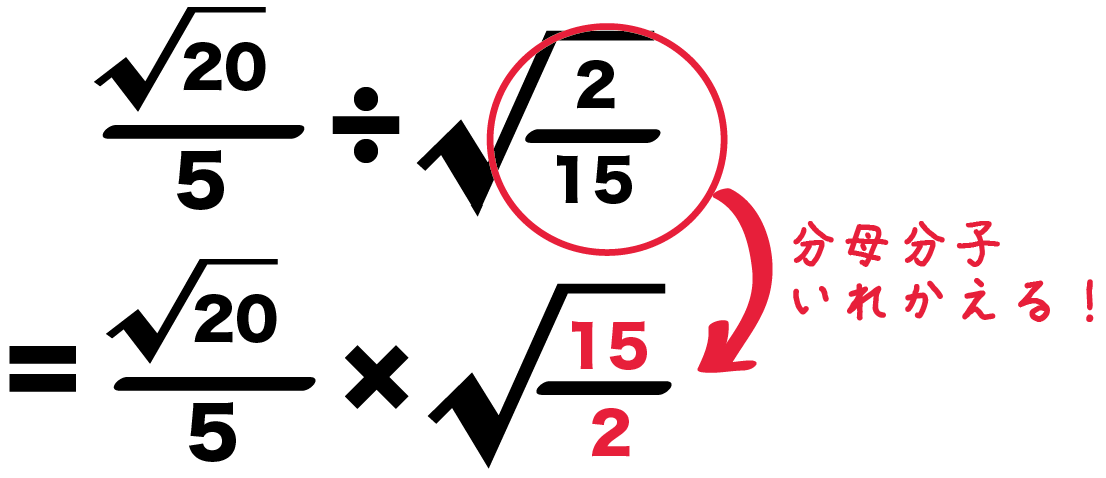



平方根の計算 ルート分数の割り算の仕方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
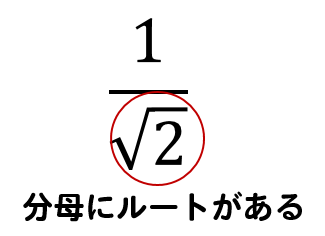



平方根 分母の有理化のやり方はこれでバッチリ 数スタ




高校数学 平方根の定義と2乗の平方根 A の基本的な扱い 受験の月



48s96ub7b0z5f Net Shisuu Keisan




平方根 平方根の加法 減法 乗法 除法 中学数学 定期テスト対策サイト



高校数学i根号を含む式の計算 この問題の 1 の解き方をいくら調べ Yahoo 知恵袋




中学3年生 数学 平方根の加法 減法 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




高校数学b 階差を利用する和 根号型 対数型 階乗型 受験の月




平方根 ルート の重要な計算方法まとめ 数学fun




平方根 ルートの計算方法まとめ 問題を使って徹底解説 数スタ




根号を含む式の計算 乗法 除法をくふうして計算する 教遊者




中学数学 平方根 のコツ 有理化 加減乗除 展開




平方根 とは何か 計算方法 覚え方 どう役に立つのかを解説 アタリマエ




中3 9 1 根号を含む式の加法 減法の計算 Youtube




有理化とは やり方を分かりやすく解説 練習問題つき 高校生向け受験応援メディア 受験のミカタ




平方根とは 東大生が平方根の計算方法や覚え方を伝授 高校生向け受験応援メディア 受験のミカタ




式と証明 1 分数式の計算 整式の割り算 数ii B 東大数学9割のkatsuyaが販売する高校数学の問題集




中学数学 平方根 整数になる自然数n の簡単なやり方 丁寧な解説 スタディーランナップ




高校 数 根号の式を含む計算2 Youtube




指数法則とは 公式 証明や 分数 ルートを含む計算問題 受験辞典
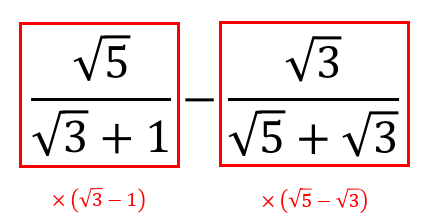



ルートの分数計算 問題解説で完全マスターだ 数スタ




根号を含む式の計算 乗法 除法をくふうして計算する 教遊者




中学3年生 数学 平方根の加法 減法 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



数iの根号を含む式の計算です 問2なのですが 公式4 5 Yahoo 知恵袋




平方根の計算 ルート分数の割り算の仕方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




式の計算 高校数学の美しい物語




根号 ルート が付いている漸化式の基本的な解き方 わかるようになる高校数学
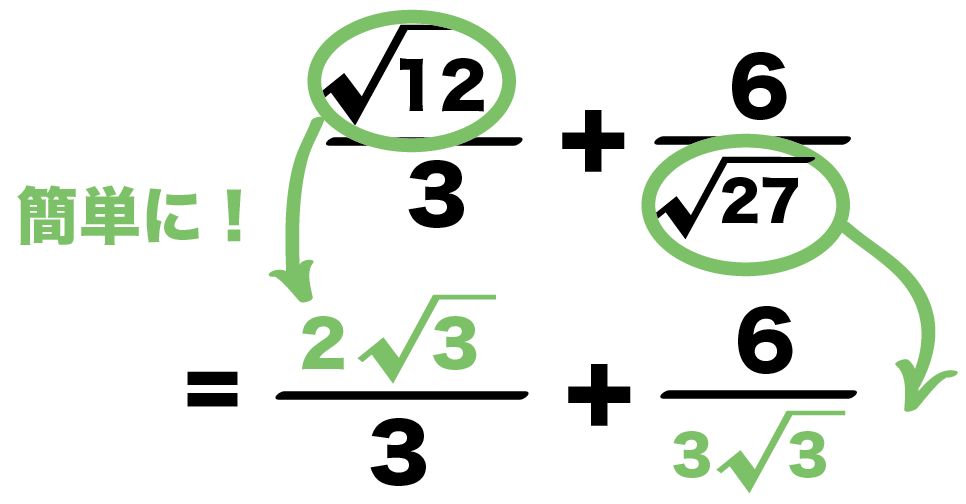



平方根の計算 ルートの分数の足し算 引き算の仕方がわかる5ステップ Qikeru 学びを楽しくわかりやすく




高校数学 因数分解 解の公式を使ってルートが登場する因数分解を解けるようになろう 数学の面白いこと 役に立つことをまとめたサイト



48s96ub7b0z5f Net Kongou Kyokugen
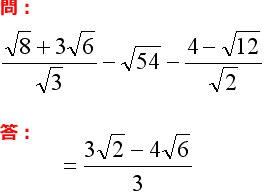



中学の数学 ルートの計算方法って Sakura Scope




中3数学 ルートのたし算 ひき算2 例題編 映像授業のtry It トライイット




改訂版 高等学校 数学i入門ノート チャート式の数研出版




根号を含む式の計算 しっしーのお計算ん向上委員会




平方根の足し算と引き算 ルート計算のやり方や分数の求め方 リョースケ大学




中学数学 平方根 ママ塾ノート




数と式 平方根について 日々是鍛錬 ひびこれたんれん




高校数学 数 13 ルート シリーズ 有理化編 Youtube



0 件のコメント:
コメントを投稿