棒に重さのあるてこをマスターしよう 辻義夫の中学受験に打ち勝つ家庭学習法
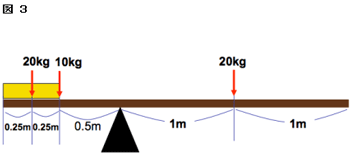
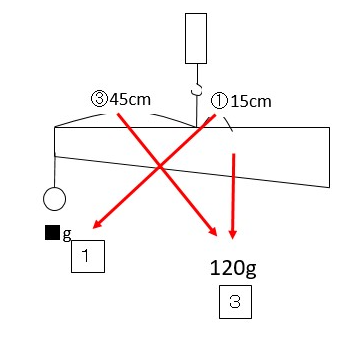
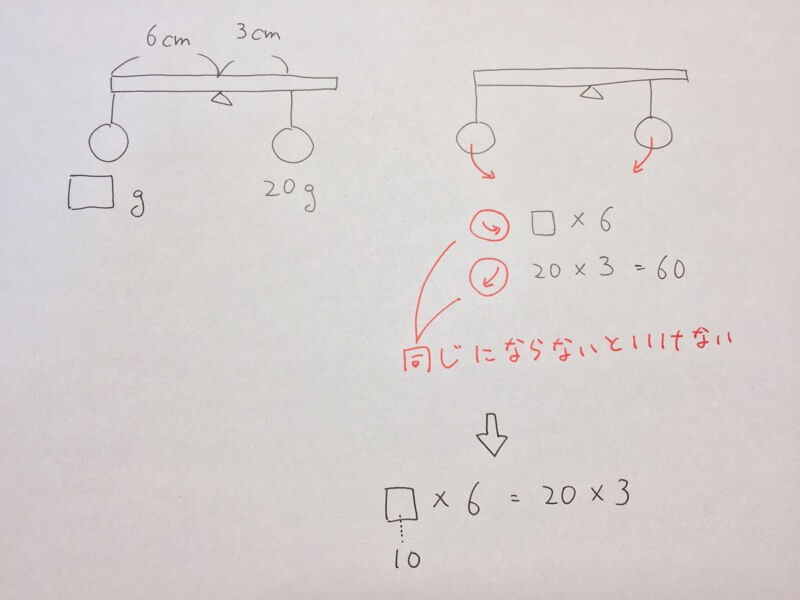
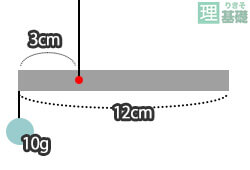
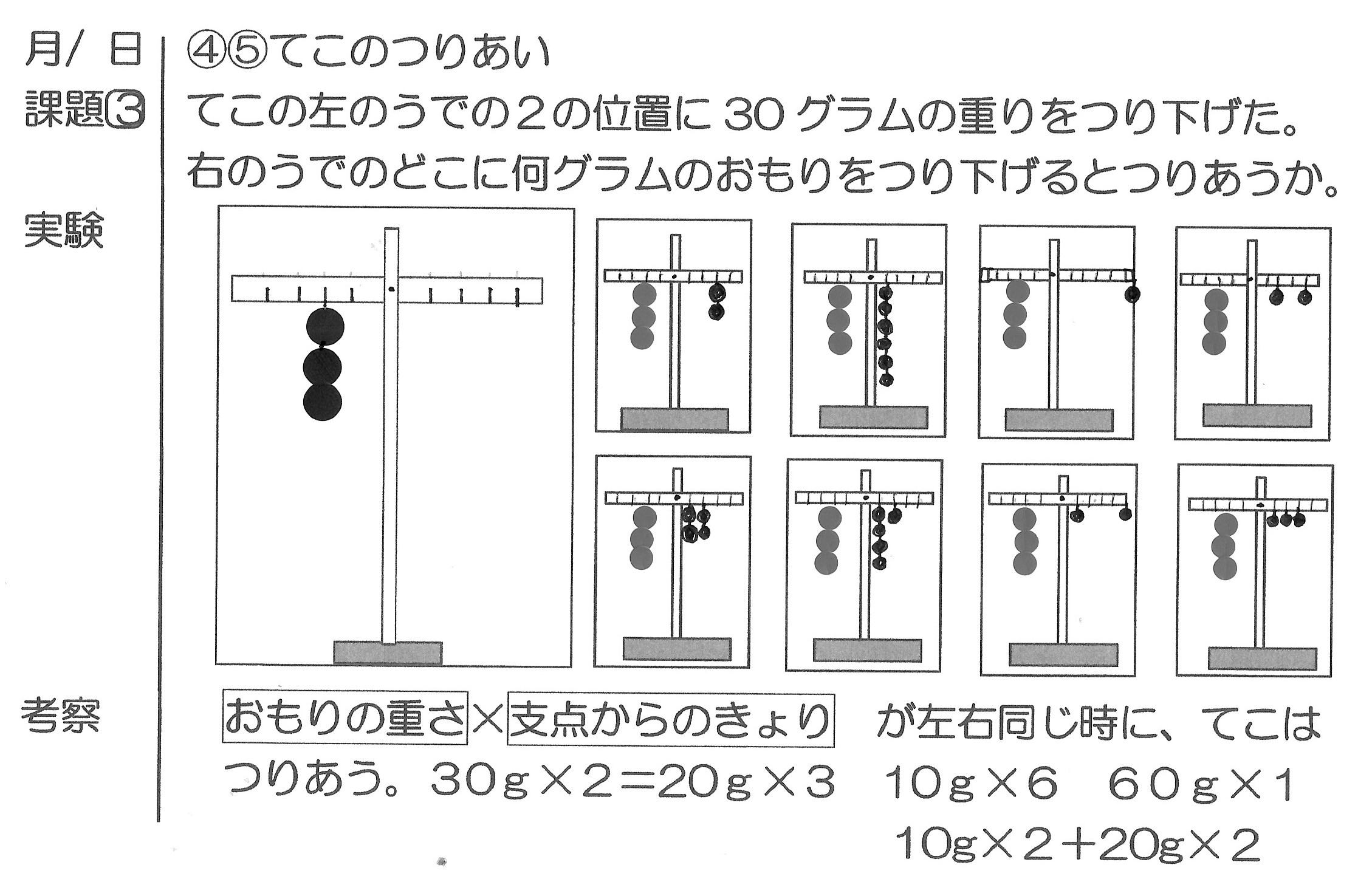
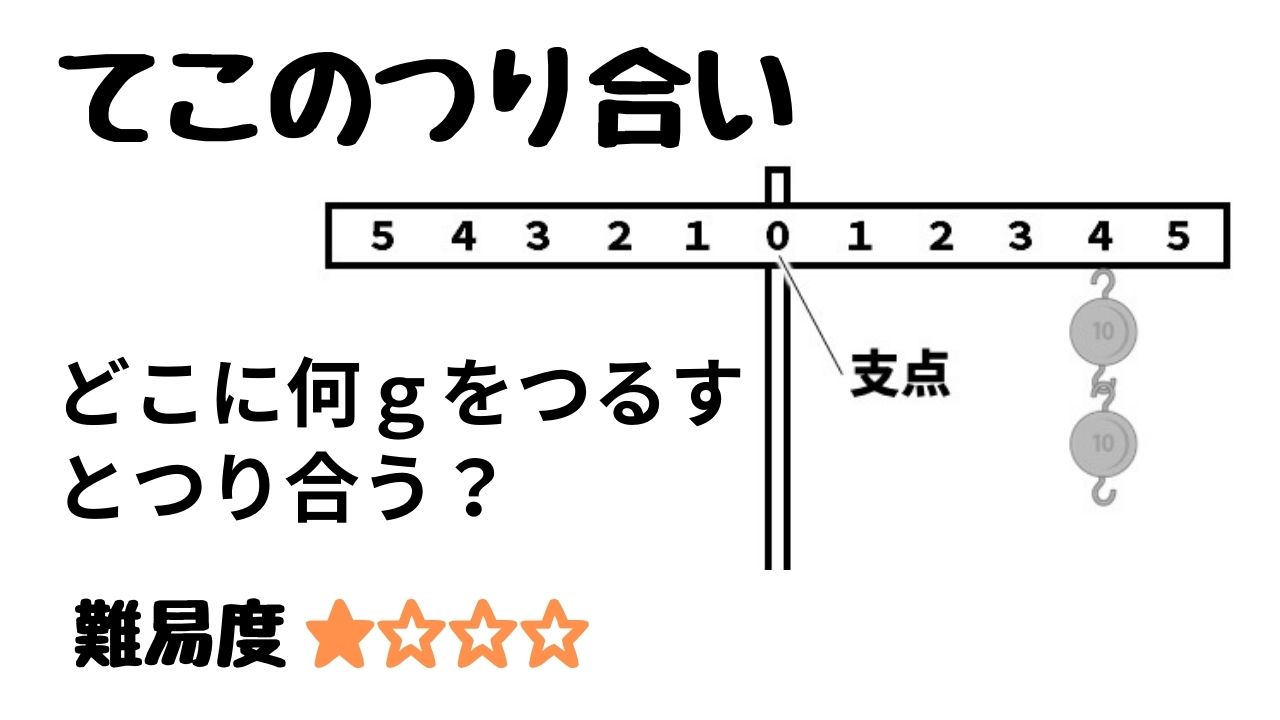
目次 「てこ」の原理の基本 てこの原理とは? てこの3点:支点・力点・作用点 てこのつり合い:「モーメント」と逆比 3つ以上の力でつりあう時の問題の解き方 支点にかかる力(上向きの力) 棒に重さがある場合 まとめ てこのつりあいの問題を解くポイント左と右のモーメントを書く、左のモーメントと右のモーメントは必ず同じになるつりあいの位置から 3cm 離れたところに g のおもりをつりしたとき、つりあいの位置から 6cm 離れたところに何 g のおもりをつるせば、つりあうでしょうか?
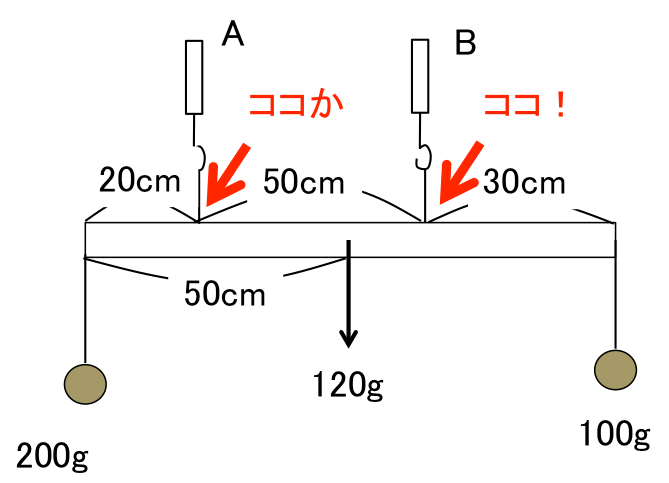
てこ つりあい 計算
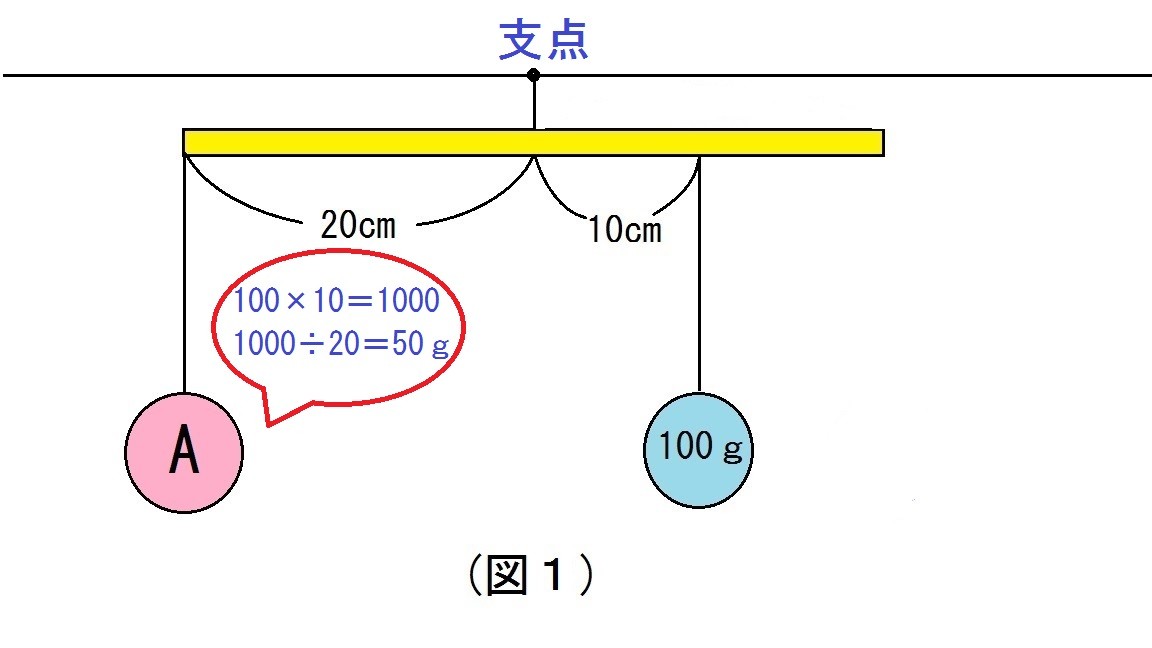
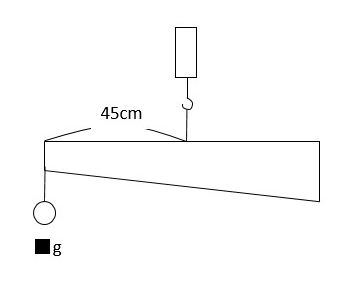
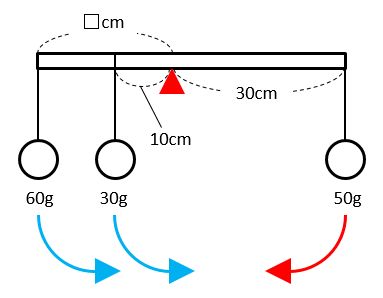
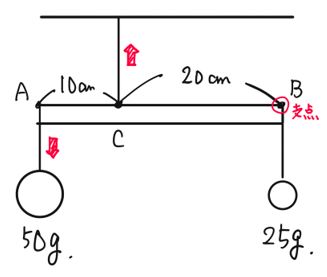
てこ つりあい 計算- つりあうためには、重さの比は逆比になるので、2 : 1 90(g) − 60(g) = 30(g) おもりC <ウ)の考え方と答え> B + D = 40 + 60 = 100(g) A + C = + 30 = 50(g) 重さの比 (B + D) (A + C) = 100 : 50 = 2 : 1 つりあうためには、支点からの距離の比は逆比になるので、1 : 2 目盛り2から目盛り8までは、目盛り6つ分あるので、それを 1 : 2 に分けると 「てこ」の公式 おもりの重さ × 支点までの距離 = おもりの重さ × 支点までの距離 これが 釣り合っている状態です。 この公式を下の図で解説すると、 A × a = B × b となります。 例題 図のてこはつり合っています。 おもりAは何gですか。 ただし、棒の重さは考えないものとします。 公式に当てはめて計算してみましょう。 A × a = B × b おもりの重さ × 支点までの距離 = おもりの
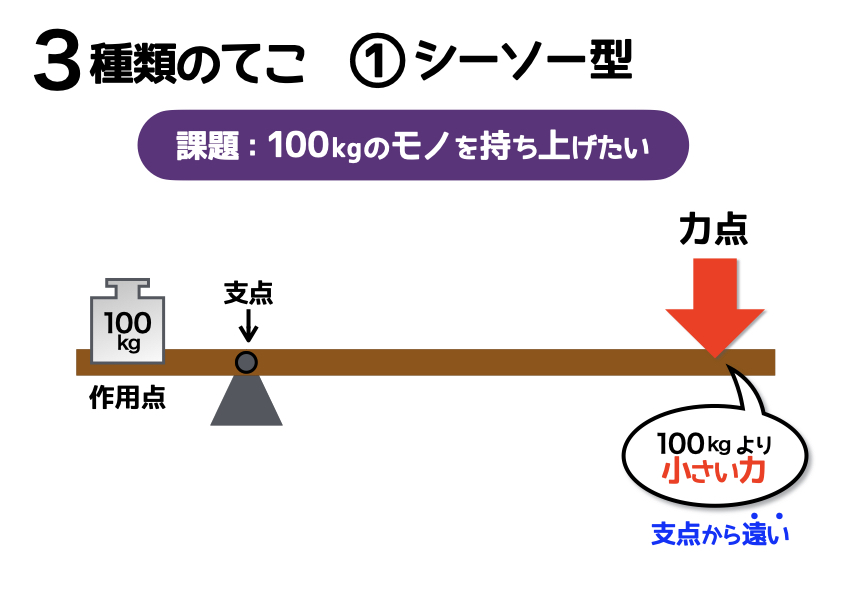
てこの原理とは 計算方法や 問題を解くための 王道アプローチ を紹介 中学受験ナビ
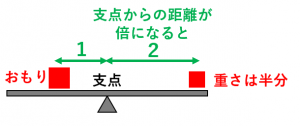
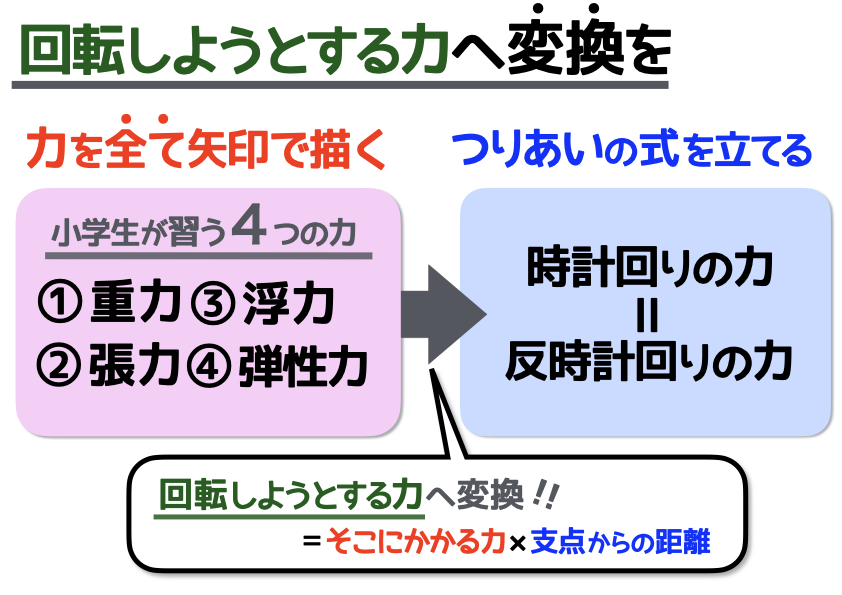
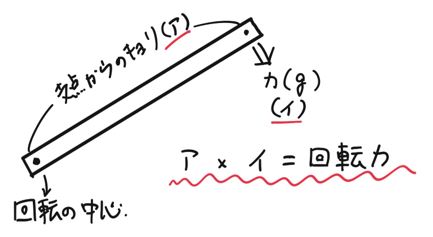
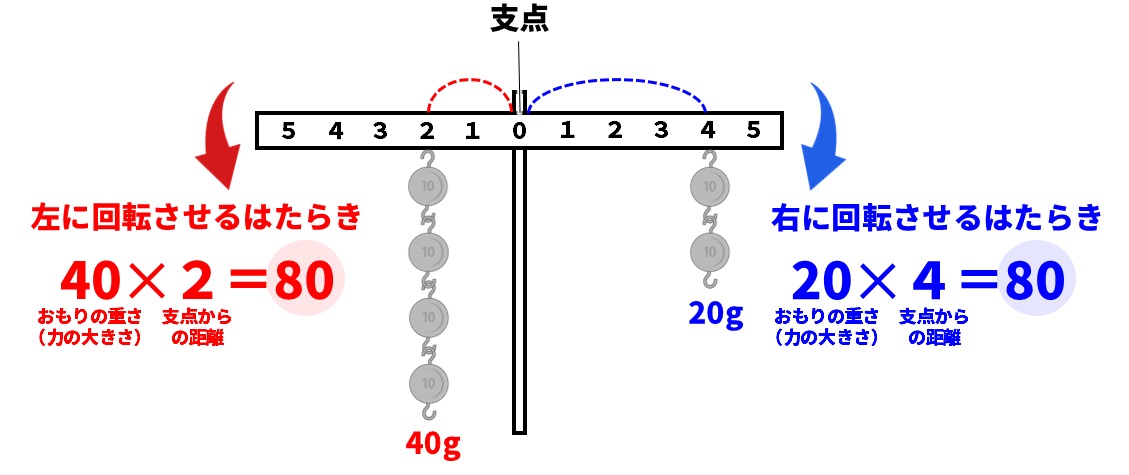
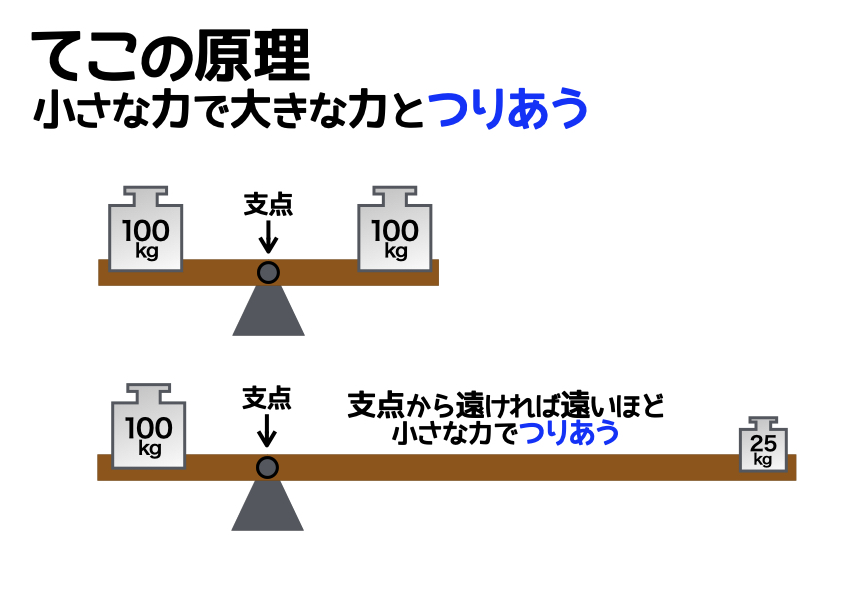
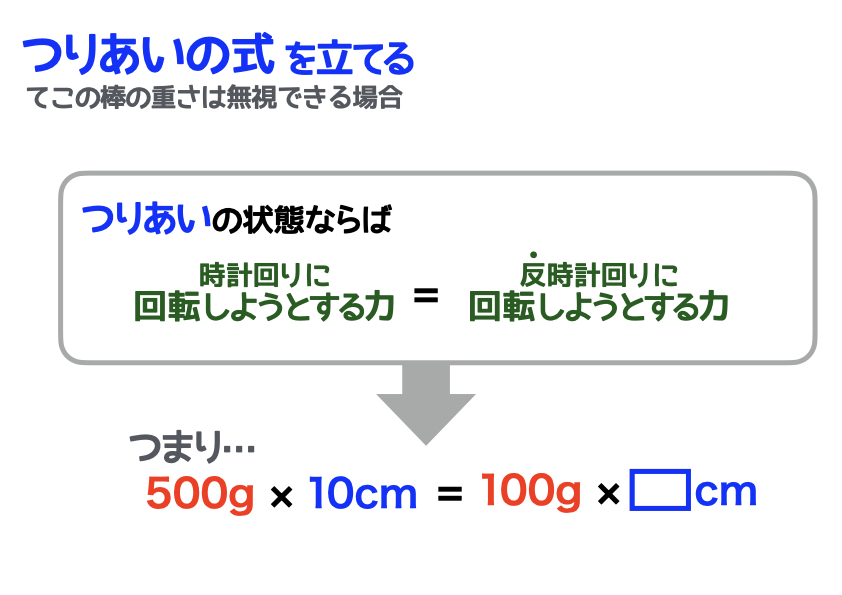
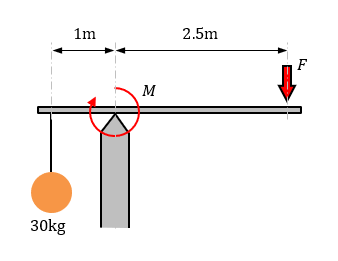
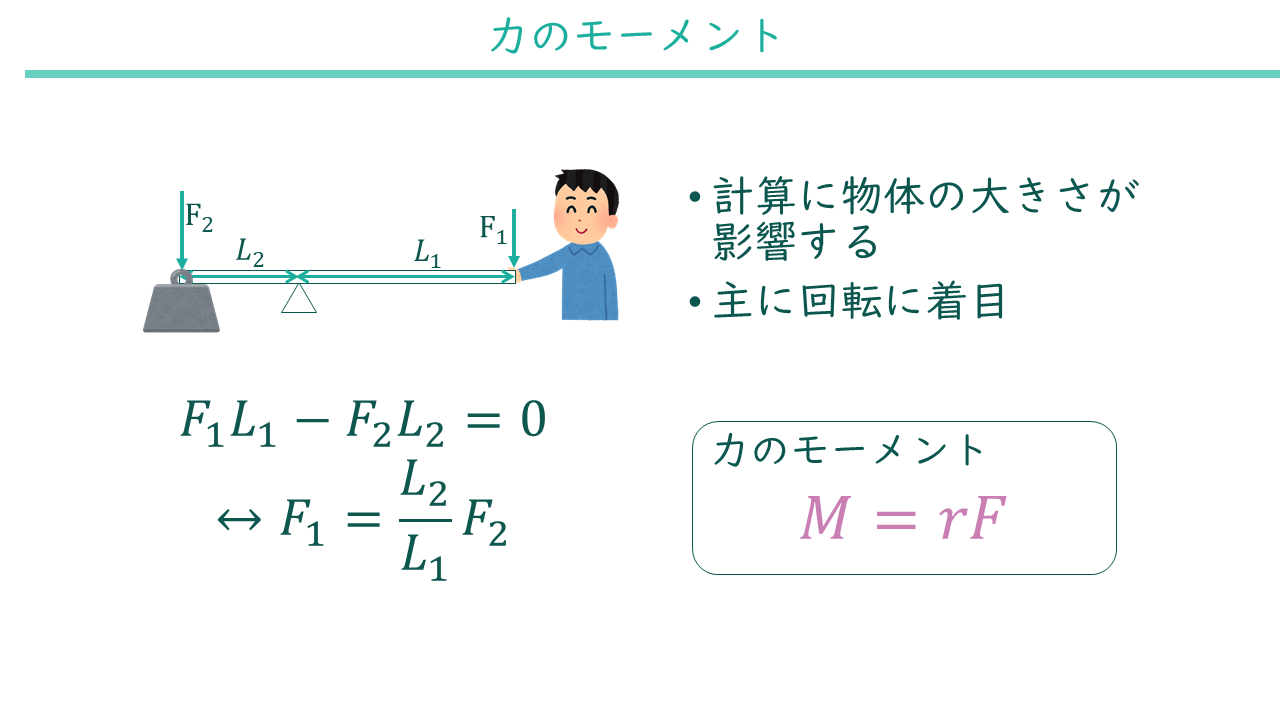
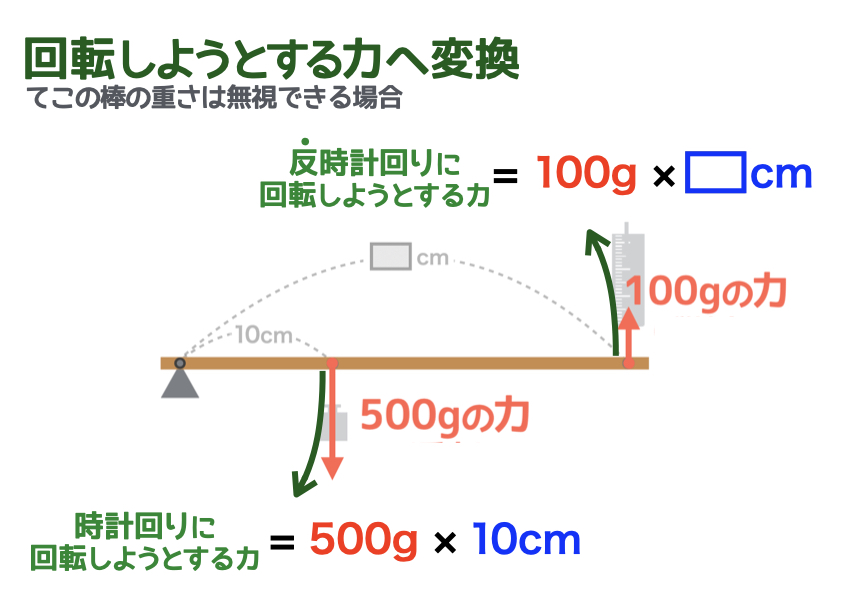
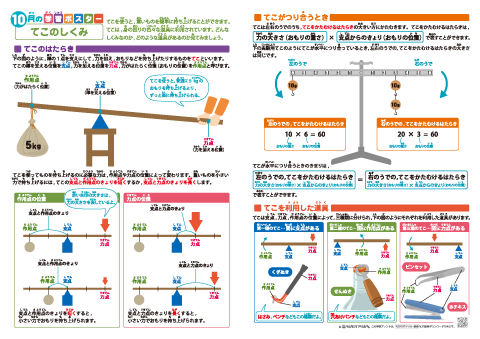
てこが水平になっているとき、左右の「てこをかたむけるはたらき」は同じ。 てこをかたむけるはたらきは、 「力の大きさ(おもりの重さ)×支点からのきょり(おもりの位置) で表すことができる。 力のつり合いや、てこの実験に使われる器具を力のモーメントをMとすれば、 M=P×L=100×30m=300 kN・m が力のモーメントです。 つまり、下図の方向(B点を起点として時計回り)に力のモーメントが発生しています。 このような問題では、どこを起点に回転するのか考えると理解が早くなりますてこのつりあいてこに力を加え、水平になるとき、 てこはつりあっているという。 右の図のような場合、水平にならないので、 てこはつりあっていない。 てこがつりあうとき、次の式が成り立つ。
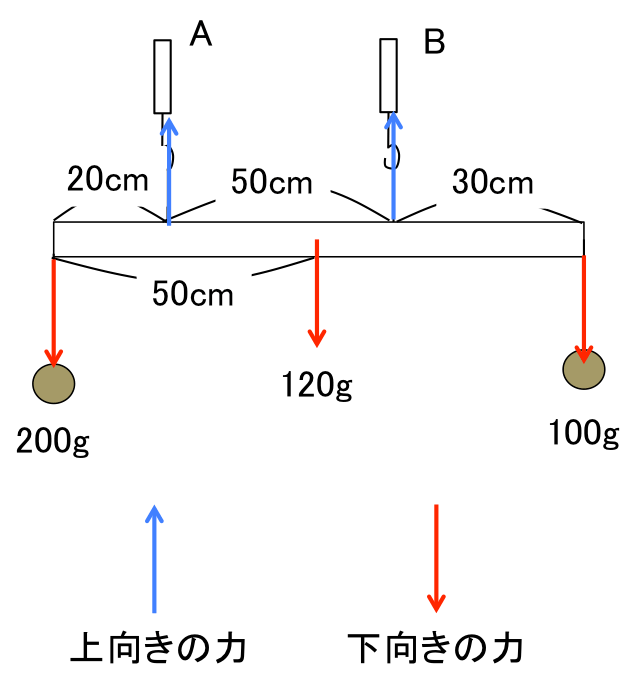
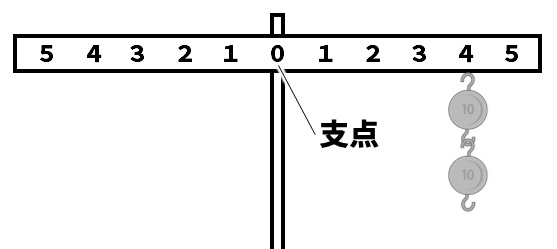
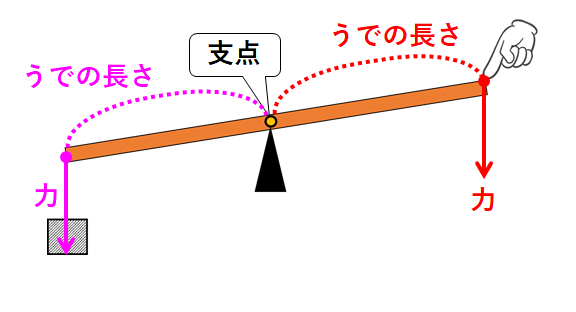
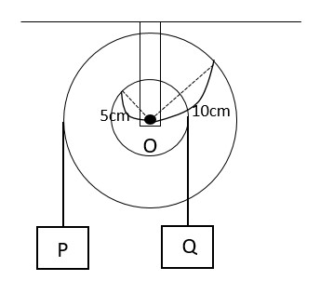
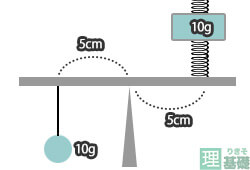
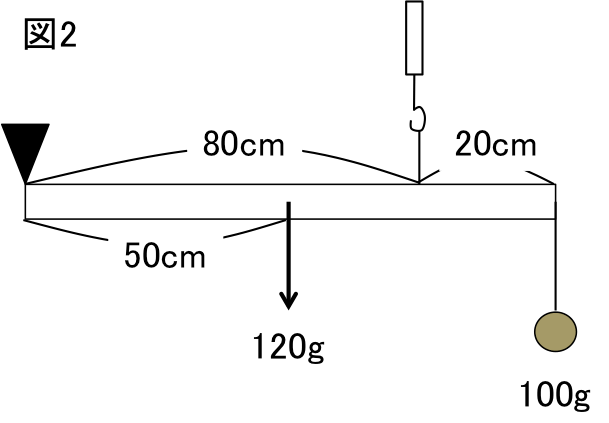
てこのつり合い 釣り合っているてこは、下向きの力と上向きの力が同じになる この図の場合は、中央に支点があります。 左側の下向きの力は 5cm×10g=50g、 右側の上向きの力となるバネばかりも 5cm×10g=50g となります。てこの原理の計算と公式、距離と反比例の関係 てこの原理の公式を下記に示します。 W×L1=P×L2 下図をみてください。 作用点に生じる力をW、作用点から支点までの距離をL1、力点に作用する力をP、力点から支点までの距離をL2とします。 では考えて
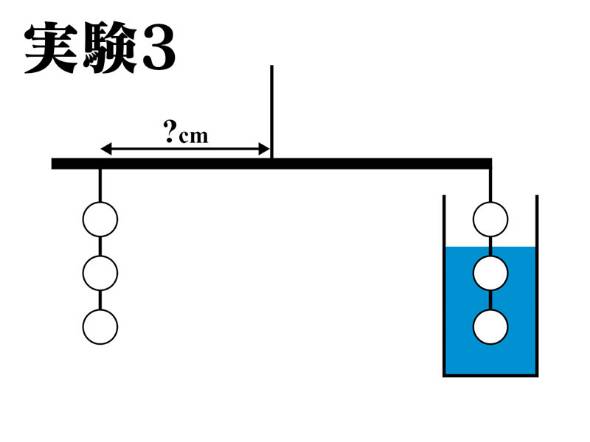
てこ つりあい 計算のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | 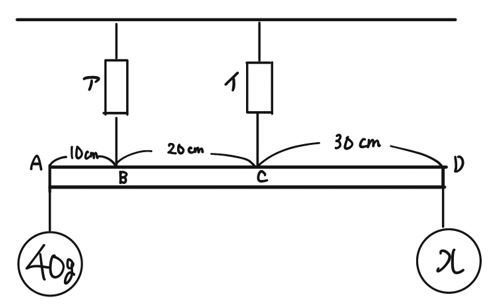 |
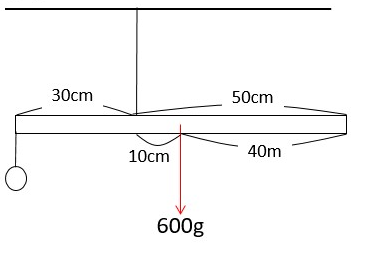 | ||
「てこ つりあい 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
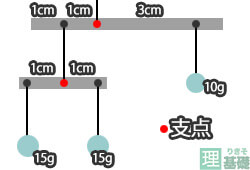 |  | 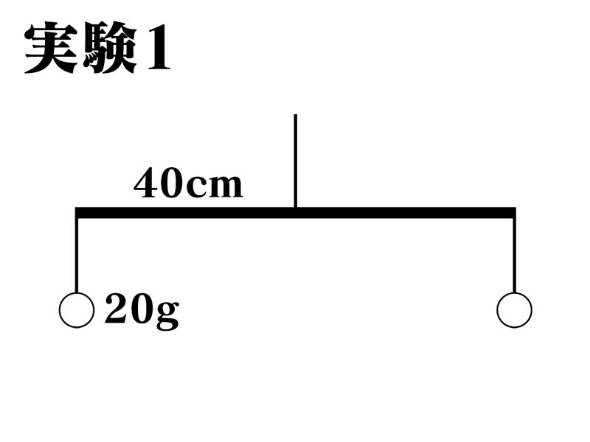 |
 | 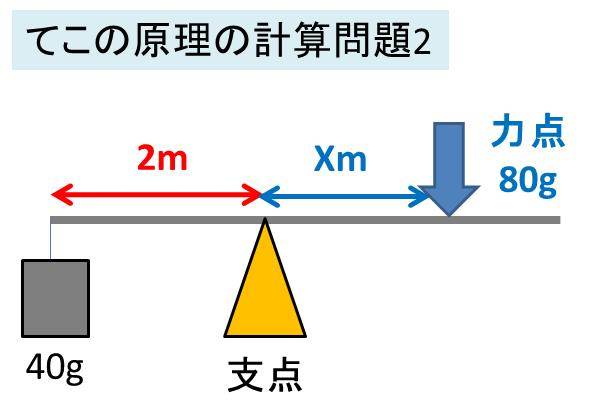 |  |
 | 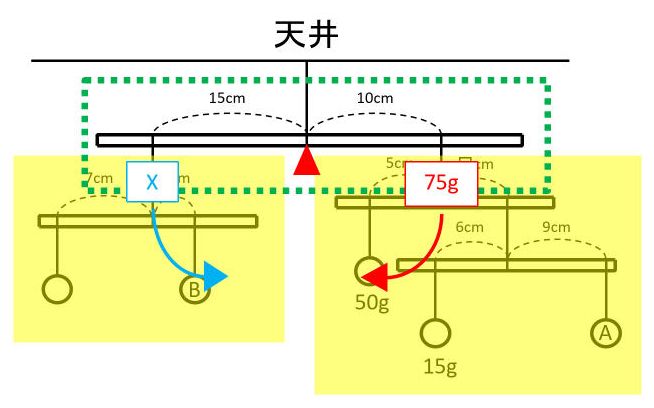 | |
「てこ つりあい 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
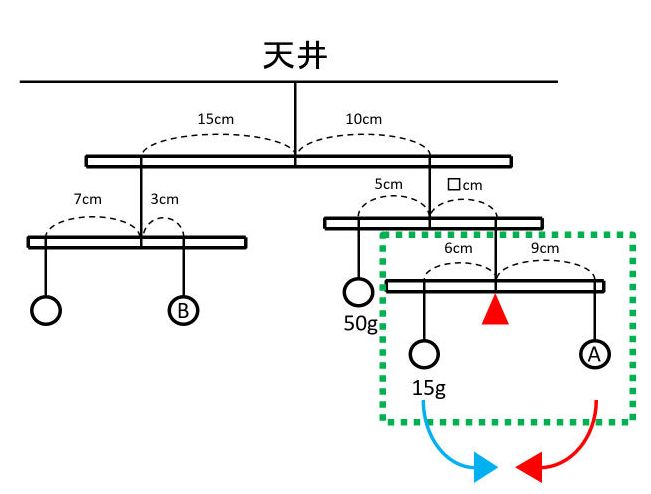 |  | |
 |  |  |
 |  |  |
「てこ つりあい 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「てこ つりあい 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | 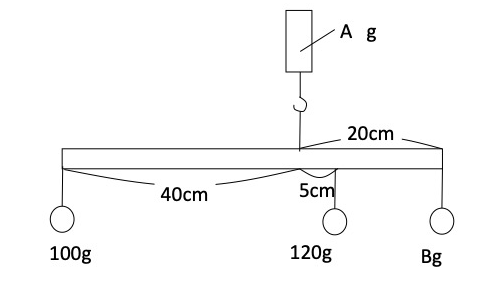 |  |
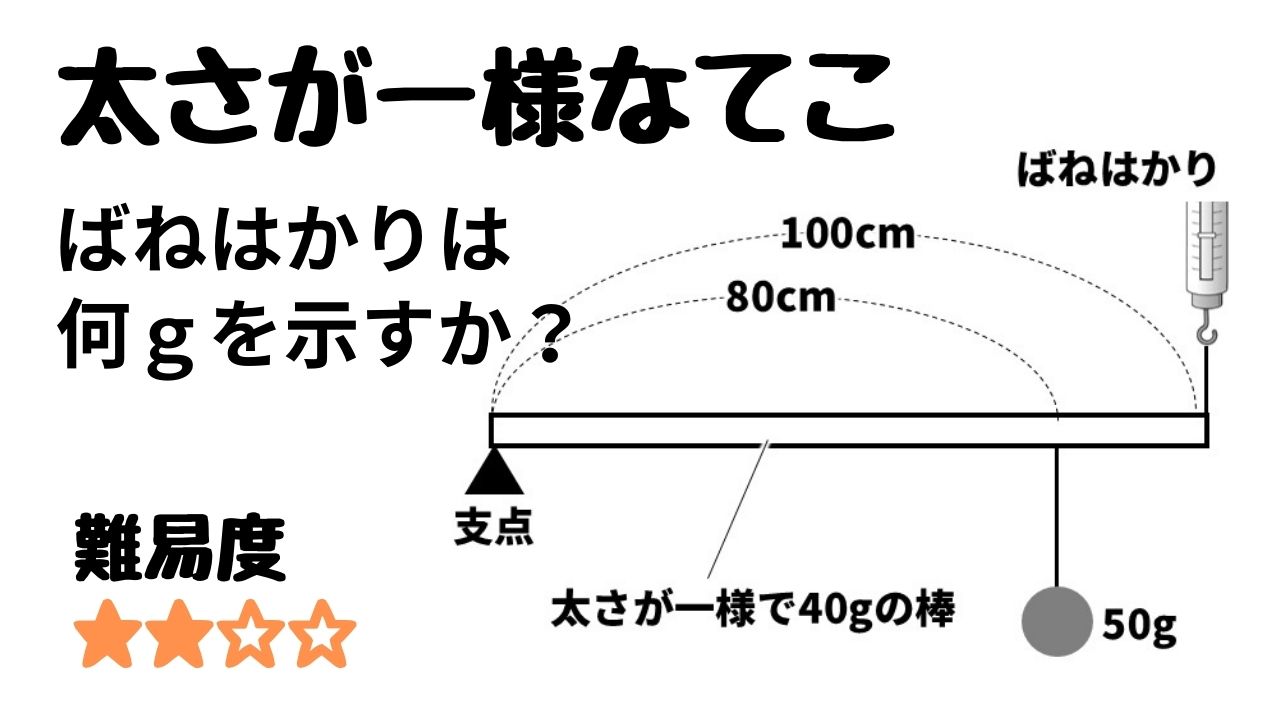 |  |  |
「てこ つりあい 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | 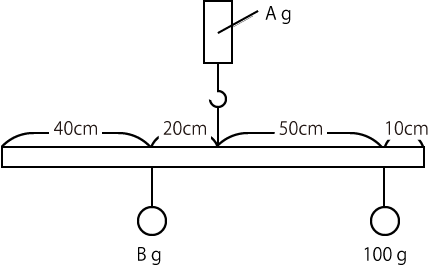 |
 |  |  |
 |  |  |
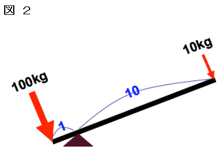
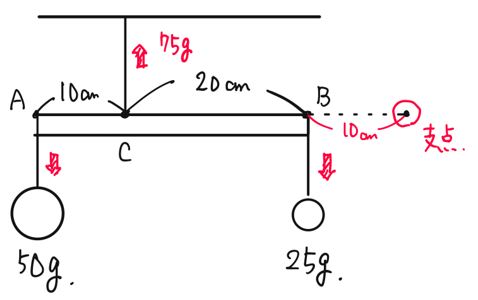
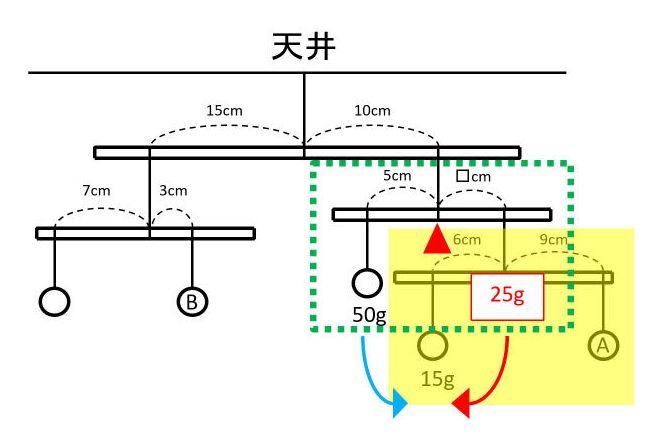
「てこ つりあい 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | 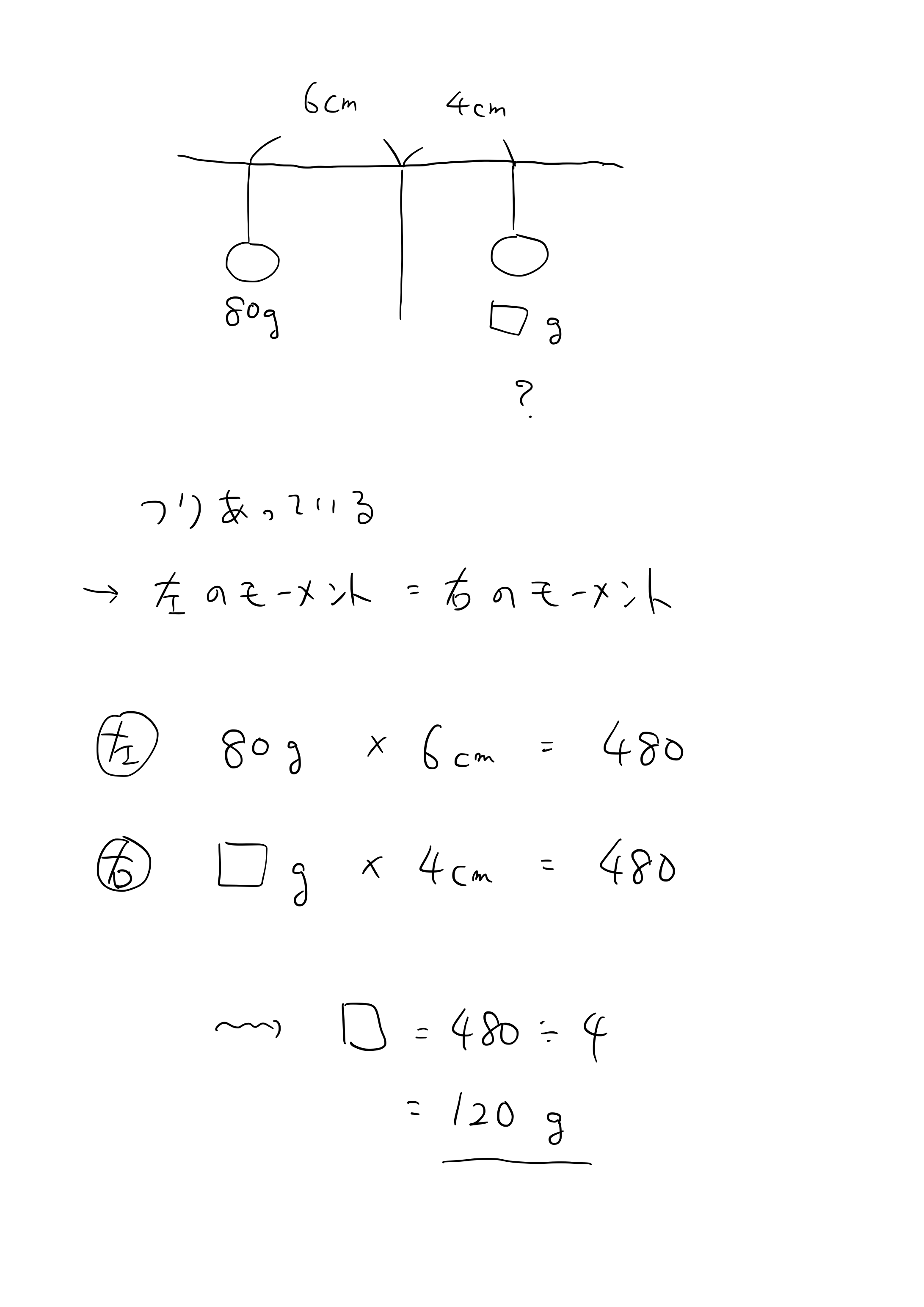 |
 |  |  |
 | 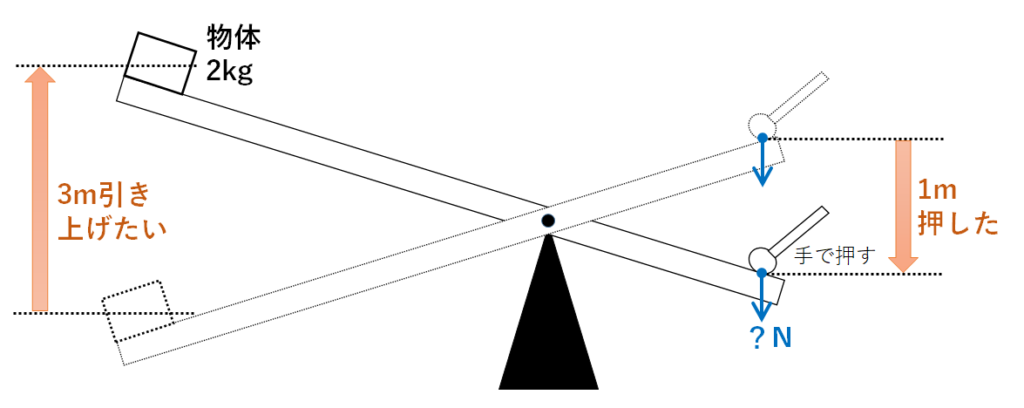 | 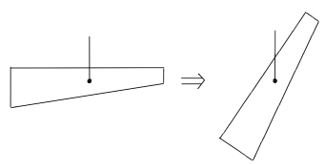 |
「てこ つりあい 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 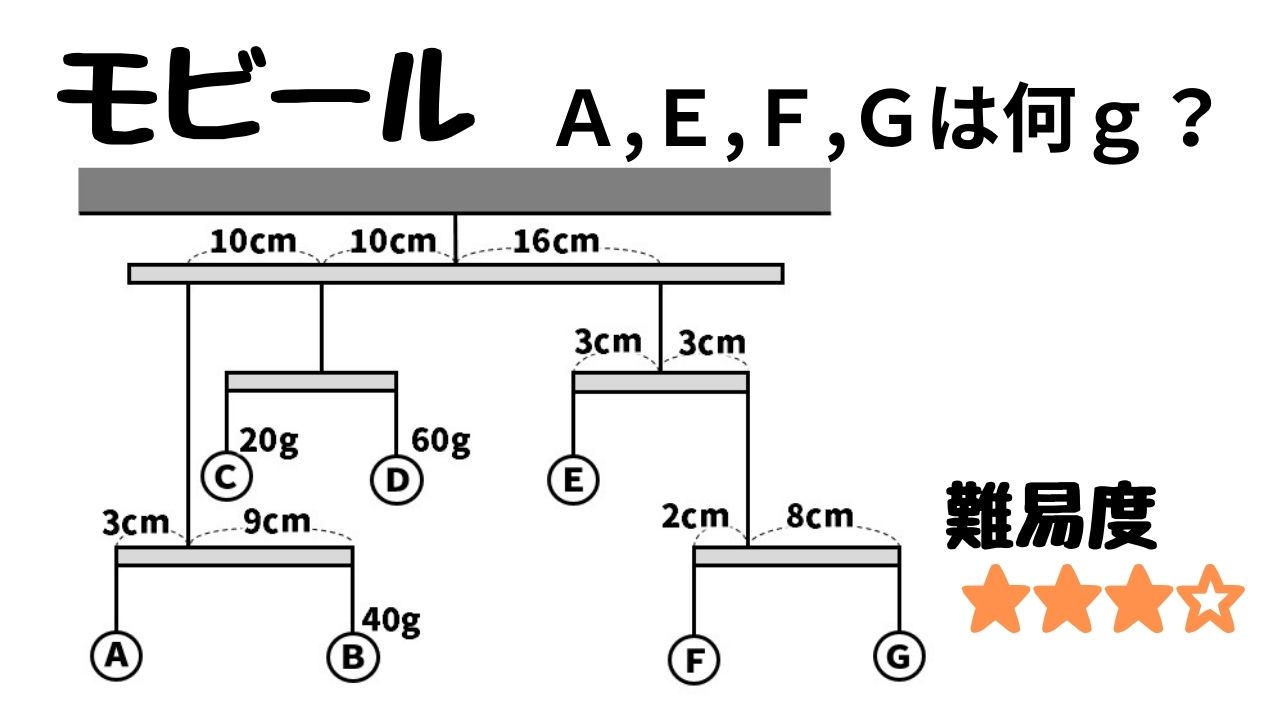 | |
 |  |  |
 |  |  |
「てこ つりあい 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「てこ つりあい 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | ||
「てこ つりあい 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | 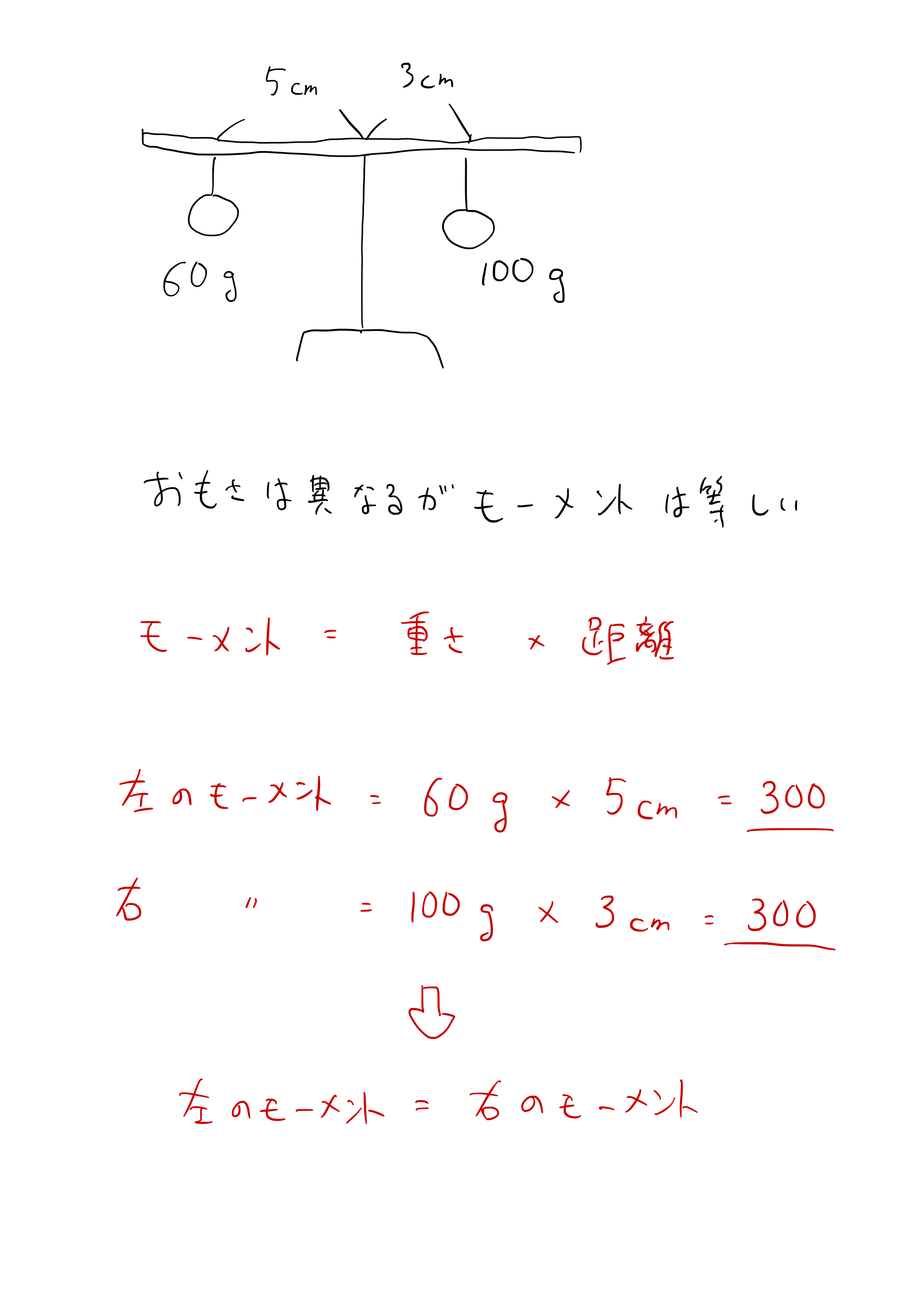 |  |
「てこ つりあい 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
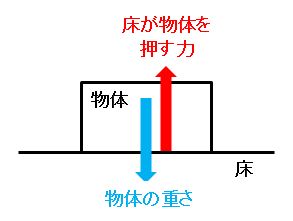 | 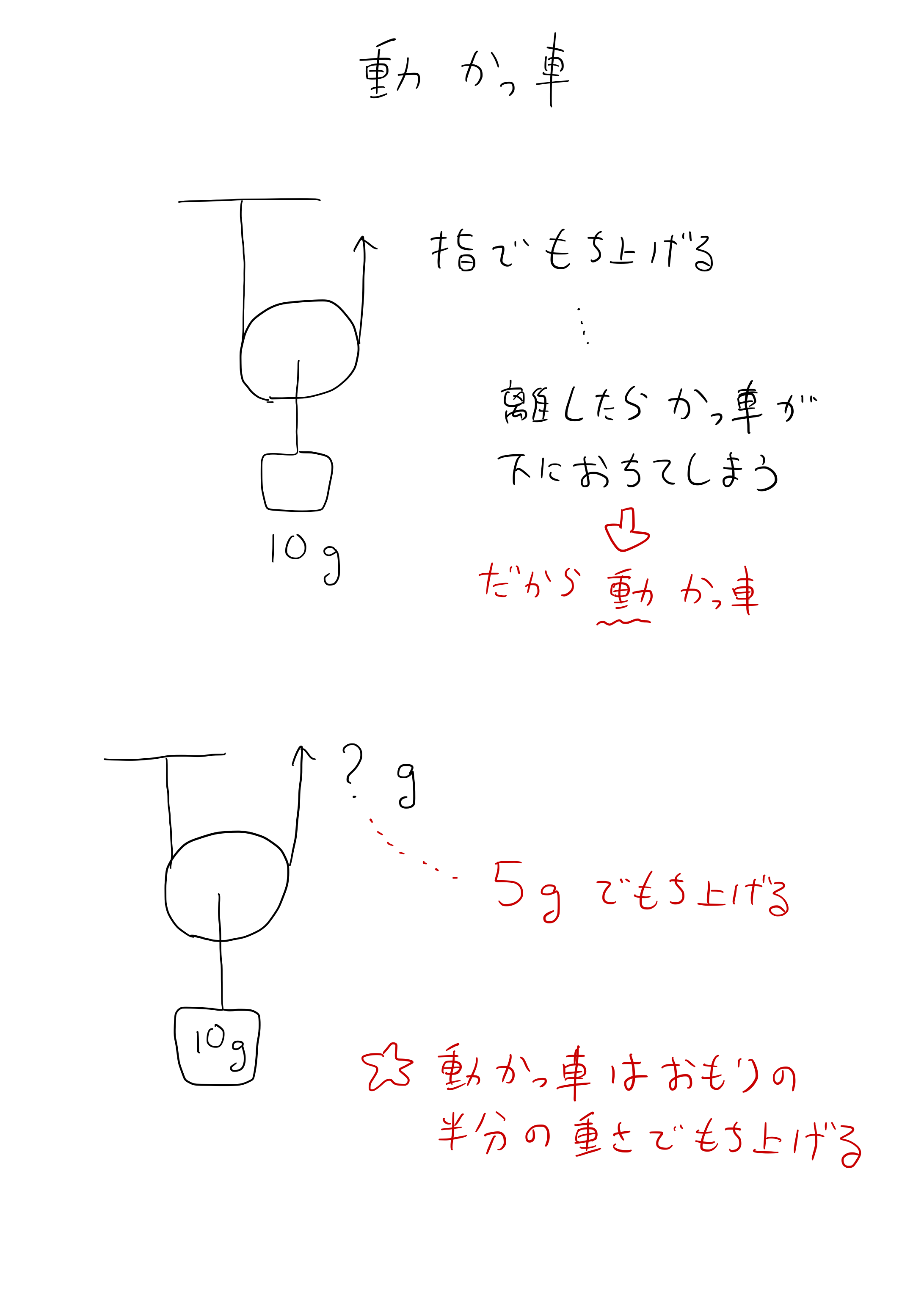 |





0 件のコメント:
コメントを投稿